Le temps et l’invention
1. Introduction
Comme physicien, je sais que toute matière est faite de simples atomes, dont la dynamique permet de comprendre la plupart des comportements observés dans la matière inerte. En revanche, la matière vivante faite des mêmes atomes ne se comporte pas du tout de la même manière, tout particulièrement dans le monde des arts et de la musique : des formes nouvelles surgissent continuellement. Le physicien ne peut justifier ces changements que s’il s’explique comment et pourquoi le nouveau se construit à partir de l’ancien. L’explication fait donc intervenir les conceptions mêmes que l’homme se fait du temps et du changement, et elles ont elles-mêmes changé maintes fois dans l’histoire de la physique.
La première conception du temps comme facteur de changement remonte à Aristote : le temps est alors conçu comme une entité contenue dans les substances ; il s’épuise quand ces substances acquièrent les formes finales qu’elles revêtent dans les êtres inertes ou animés. Il faut reconnaître que cette conception se rapproche de la perception immédiate : nous voyons bien que le temps préside à l’évolution irréversible des êtres vivants vers la complexité, et que cette complexité culmine dans les activités mentales individuelles ou culturelles. Parfois avec réticence, nous admettons aussi que l’évolution est soumise à des téléonomies vers des formes finales qui devraient à la longue aboutir à un monde idéal. Le problème est d’expliquer comment ces formes s’établissent durablement dans un monde réel fait d’atomes, et par ailleurs très instable et désordonné.
Or, la physique a rencontré un problème semblable lorsqu’il s’agissait de rendre compte de la présence d’ordre dans la matière cristalline : on voit une forme régulière et étendue qui s’impose d’elle-même, bien qu’elle paraisse très improbable au premier abord. La solution de ce problème a passé par un changement radical de la conception du temps : il est vu désormais comme extérieur aux choses, et il s’écoule spontanément quels que soient les événements. De ce changement est résultée la dynamique classique de Newton qui s’applique aux atomes composant la matière. Ensuite, la thermodynamique a montré que l’évolution spontanée vers l’ordre entre atomes a une échelle de temps spécifique. C’est pourtant une acquisition récente car un problème conceptuel se présente, bien plus difficile que la simplicité de la matière ne l’aurait laissé supposer.
Aujourd’hui, ce même chemin reste à faire pour les formes très complexes apparaissant dans les sciences de la vie et les arts, mais le succès remporté par la physique peut nous servir au moins de modèle : il en résulte une théorie macroscopique pour les systèmes complexes appelée morphodynamique. Elle formule un principe d’évolution vers la forme nouvelle dans un temps spécifique de ces systèmes. Cette théorie a aussi l’intérêt de se prêter à une interprétation cognitiviste : elle reconnaît la place due à la signification et à l’invention dans l’activité mentale, par exemple telles qu’on les trouve dans l’expression musicale.
Pour le montrer, cet article examine d’abord la dynamique des composants de la matière inerte et de la matière vivante pour en faire ressortir les ressemblances et les différences. L’analyse passe ensuite aux systèmes de nombreux composants ; à ce niveau, l’isomorphisme avec la physique est complet et il permet de tracer le chemin par lequel les systèmes mentaux acquièrent la nouveauté. Il en ressort le rôle central des systèmes symboliques dans l’évolution socio-culturelle, y compris dans la musique.
2. Dynamique des particules physiques
La physique élémentaire veut que deux variables-clefs soient nécessaires pour décrire le mouvement d’une particule : une variable de configuration et une variable de flux. La première est la position qu’il s’agit de prédire en fonction du temps, l’autre est la quantité de mouvement qui mesure le flux temporel de matière se déplaçant sous l’effet de la force appliquée. Il y a donc un ensemble de quatre grandeurs en jeu, et on conjecture qu’elles sont reliées par des équations dynamiques spéciales et dites équations de Newton (voir Appendice p. 97). Cette conjecture se base d’abord sur notre conception intuitive du temps qui n’est nullement objective, mais on constate après coup que l’expérience la confirme pleinement. En particulier, certaines forces simples donnent lieu à des solutions périodiques qu’on peut vérifier exactement dans les horloges. De la sorte, on s’est construit une définition opérationnelle : le temps physique est la variable qui rend prédictives les équations dynamiques de Newton et qui est mesurable par les horloges physiques.
3. Dynamique des structures fonctionnelles
Concernant les organismes complexes, la première démarche est d’identifier les composants qui concourent à leur métabolisme. Or, on constate la présence à tous les niveaux de la dualité structure-fonction : un élément structurel ne s’établit durablement que s’il répond aux stimuli externes par au moins une fonctionnalité utile à l’adaptation de l’ensemble. On en déduit que les composants des organismes agissent comme des structures fonctionnelles (Fig. 1) qui ont une dynamique décrite par deux variables-clefs : une variable de configuration caractérisant la structure et une variable de flux caractérisant la fonction. La première est donc un paramètre d’ordre qui indique si la structure est disponible ou non pour répondre au stimulus, la seconde est la fonction produite qu’il s’agit de prédire au cours du temps. A nouveau, un ensemble de quatre variables se présente, et on conjecture que des équations dynamiques appropriées décrivent les relations mutuelles entre ces variables (Voir Appendice p. 97). L’expérience confirme pleinement cette conjecture comme elle l’a fait en physique.

Figure 1 : Structure fonctionnelle. Composant des systèmes complexes fermés par une frontière, elle se caractérise par un paramètre d’ordre x, qui détermine la production d’un flux p vers l’extérieur. Le paramètre d’ordre transite entre deux valeurs stationnaires lorsque l’influence externe I passe par des valeurs critiques lors de ses variations aléatoires dans le temps.
En particulier, certains stimuli simples donnent lieu à des solutions périodiques ; or, on constate que les horloges biologiques existent en grand nombre dans le monde vivant : le nerf, le pouls cardiaque (Zeeman 1972) et les cycles circadiens (Winfree 1987) sont des exemples bien étudiés. Mais il existe aussi des horloges abstraites sous la forme de structures temporelles répétitives : on en trouve en musique ou en poésie, par exemple les rythmes, les mélodies, le chant canon et les vers scandés ; on en trouve aussi dans la communication sous la forme de profils tension-résolution et de tours de parole, ou en économie sous forme de cycles. Toutes ces horloges attestent la pertinence de la conjecture : les structures fonctionnelles obéissent à des équations de même forme jusqu’aux plus hauts niveaux de complexité. En conclusion, on a construit pour ces structures une définition opérationnelle du temps qui est logiquement indépendante du temps physique : le temps complexe est la variable qui rend prédictives les équations dynamiques des structures fonctionnelles et qui est mesurable par les horloges biologiques ou abstraites.
4. L’isomorphisme avec la physique
L’observation met ainsi en évidence une coïncidence formelle entre matière vivante et matière inerte : il faut deux variables-clefs dynamiquement liées pour décrire les composants, qu’ils soient des structures fonctionnelles dans le premier cas ou des particules matérielles dans l’autre. La physique n’exige en rien cette coïncidence mais elle a des conséquences considérables : comme les équations ont la même structure mathématique, elles imposent un isomorphisme général entre les êtres vivants et les êtres inanimés sans requérir que les variables dynamiques des uns soient rationnellement liées à celles des autres. Au contraire, les équations impliquent dès l’abord des définitions opérationnelles du temps qui sont indépendantes. Cette indépendance logique est d’ailleurs conforme à notre perception immédiate : les phénomènes observés dans les organismes n’ont pas de relation de filiation évidente avec les processus physiques sous-jacents. Il en ressort par conséquent une théorie totalement autonome, la morphodynamique : elle revendique pour la vie des conceptions spécifiques qui n’empruntent rien à la physique, mais ces conceptions présentent des relations formelles isomorphes à celles rencontrées entre concepts physiques. La théorie ne se réduit donc pas à une analogie exploitant ces concepts à titre de métaphores ; elle a au contraire la même ambition originelle que la physique : non seulement identifier les grandeurs significatives pour les êtres vivants mais encore évaluer celles qui sont quantifiables. Par exemple, le temps physique et le temps complexe ont des relations numériques qui dépendent des phénomènes très divers mis en jeu dans les organismes : le problème intéresse surtout la biochimie. Plus près des sciences humaines, la macroéconomie donne lieu à des quantifications jusqu’ici argumentées qualitativement, mais la morphodynamique est capable de les prédire avec la rigueur coutumière des sciences exactes.
D’emblée, l’isomorphisme présente une particularité capitale : les variables de flux et de configuration sont croisées dans les équations ! La raison tient à la nature profonde des composants qu’envisagent la physique et la biologie : si tous exigent deux variables-clefs, ils n’ont pas la même causalité en cascade à partir des influences externes. En effet, tandis qu’en physique les forces modifient d’abord les flux de matière qui déterminent ensuite les positions, les stimuli en biologie modifient d’abord les structures qui déterminent ensuite les fonctions exécutées. Par exemple, une synapse active change d’abord la polarité d’un nerf récepteur, ensuite celui-ci accroît l’émission d’influx. Du point de vue théorique, le croisement est purement formel mais il donne la clef d’interprétation lorsqu’on applique le modèle physique aux êtres vivants : ce que le modèle établit pour les positions vaut pour leurs fonctions, et ce qu’il établit pour les flux de matière vaut pour leurs structures. Les conséquences seront catégoriques même si elles semblent lointaines et inattendues, car notre longue expérience de la physique les rend indubitables.
5. Dynamique des systèmes physiques
Les systèmes physiques sont définis comme de très grands ensembles de particules en mouvement constant et en interaction mutuelle. D’emblée, la complication est si démesurée qu’il faut abandonner toute idée d’en calculer l’évolution : on ne la peut prédire qu’à partir de quelque conjecture non-rationnelle mais raisonnable, et elle se justifiera en dernier ressort par ses conséquences consonantes avec la réalité. Or, l’observation immédiate suggère que les particules ont des interactions répulsives qui les empêchent de s’interpénétrer ; elles entrent ainsi en collisions successives, et comme l’ouverture du jeu de billard le montre, ces collisions tendent à remplacer toute trajectoire bien définie par une multitude d’autres non-coordonnées. La conjecture est donc qu’aucun mouvement privilégié ne subsiste : un chaos général s’installe progressivement et spontanément jusqu’à ce que le plus grand désordre se réalise où plus rien ne change globalement. Il en résulte la théorie connue sous le nom de thermodynamique, et dont l’accord avec l’expérience ne fait aucun doute : la consonance avec la réalité est établie. Selon cette théorie, l’activité aléatoire des systèmes physiques se mesure donc par leur température et l’évolution s’y déroule à l’échelle du temps thermodynamique qui dépend des interactions : elle donne accès à un état d’équilibre à désordre maximal à la fois dans les deux variables-clefs, ici les positions et les vitesses. Pendant ce temps, les systèmes sont en outre susceptibles d’échanger de l’énergie avec les systèmes externes sous deux modalités : l’une est ordonnée, à savoir le travail mécanique, l’autre est non-ordonnée et reconnue comme la chaleur.
Par ailleurs, on observe que les particules ont aussi des interactions attractives qui tendent à coordonner les positions comme on le voit dans les cristaux. De façon à préserver la conjecture initiale qui prévoit correctement la tendance au désordre total, on en fait une complémentaire affirmant que l’ordre interne peut grandir à condition que l’échange d’énergie simultané désordonne davantage l’extérieur. C’est effectivement ce que l’on observe, mais il faut remarquer que, nonobstant l’ordre spatial qui s’installe, le désordre dans les vitesses subsiste et conserve son lien initial avec la température (Fig. 2) : c’est dans cette conjonction très particulière d’ordre et de désordre que résidait la difficulté conceptuelle ; seule la physique peut démontrer clairement cette conjonction et nous allons la retrouver inchangée dans les systèmes complexes.
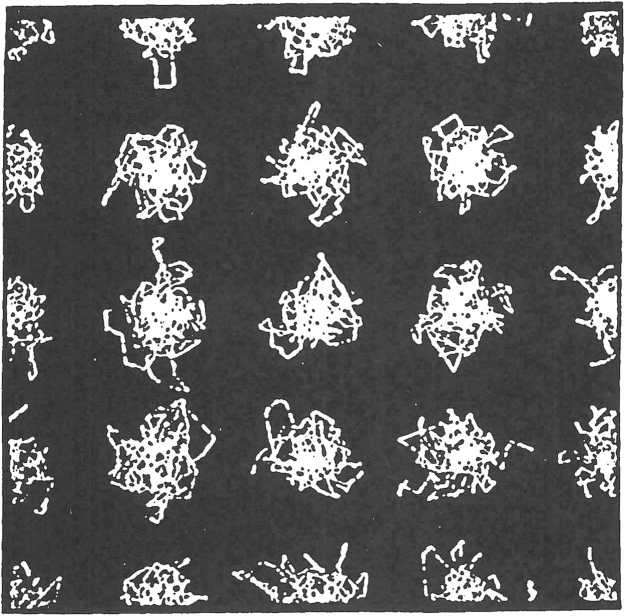
Figure 2 : Trajectoires atomiques dans un cristal. Simulation à l’ordinateur de particules en interaction à basse température : les positions sont effectivement corrélées autour des sites cristallins, mais les vitesses restent aléatoires et variables avec la température.
6. Dynamique des systèmes complexes
Les systèmes complexes sont définis comme de grands ensembles de structures fonctionnelles en activité constante et en interaction simultanée entre elles et avec l’extérieur. L’exemple type est le cerveau formé de neurones générateurs d’influx nerveux : ils sont interconnectés par les synapses excitatrices ou inhibitrices qui transmettent ces influx, mais certains neurones sont en outre liés à l’extérieur par le truchement des organes sensoriels et moteurs (Fig. 3).

Figure 3 : Système complexe. Ensemble fermé de structures fonctionnelles en interaction mutuelle et couplées aux influences externes non-corrélées caractéristiques de l’environnement réel ; l’activité stochastique interne est repérée par la température complexe T.
Dans cet exemple, les composants sont donc structurellement indépendants mais ils s’influencent par les influx qu’ils émettent, c’est-à-dire par l’intermédiaire de leurs fonctions. C’est la confirmation empirique que la clef d’interprétation joue pour les systèmes complexes : le croisement des variables exige en effet que l’interaction y dépende des variables de flux et non de configuration, et qu’elle ait des parts répulsive et attractive. On peut donc interpréter la part répulsive comme celle qui empêche que deux structures remplissent la même fonction ; elles sont donc en compétition ou en dépendance inhibitrice. Au contraire, la part attractive favorise la succession de fonctions complémentaires qui sont alors en coalition ou en dépendance excitatrice. Or, ces termes s’utilisent couramment en biologie tant dans la notion de sélection par les interactions entre espèces et individus (Dawkins 1991) que dans celle de développement organique par interactions entre cellules (Edelman 1987). Mais on trouve les mêmes termes dans les sciences humaines où la concurrence a un rôle de sélection, et qui vont de l’économie (Boulding 1981) à l’épistémologie des sciences (Robinson 1975). L’ubiquité de ces termes atteste que la présente théorie a la pertinence voulue pour décrire nombre de systèmes complexes ou abstraits.
Bien entendu, ces systèmes sont d’emblée si compliqués qu’il faut comme en physique abandonner toute idée de calcul : on ne peut prédire l’évolution globale qu’à partir de quelque conjecture non-rationnelle mais raisonnable, et basée sur l’observation immédiate. Dans cette conjecture vient figurer le fait originel que les systèmes vivants confrontent un environnement imprévisible : les structures liées à l’extérieur tendent donc à importer dans le système le chaos existant naturellement dans cet environnement ; ensuite, les interactions tendent à diffuser ce chaos dans l’entier du système, et toute coordination temporelle ne peut que se dissiper. La conjecture est par conséquent la même qu’en physique : un chaos général s’installe progressivement et spontanément, et l’activité aléatoire est mesurable par une variable globale dite température complexe. Cette conjecture achève l’isomorphisme annoncé : à partir de la thermodynamique des systèmes physiques fermés, il fonde la morphodynamique comme théorie des systèmes vivants dans leur environnement naturel.
Le premier résultat est qu’un système complexe évolue aussi à une échelle de temps propre, appelé morphodynamique, temps qui dépend tant des interactions internes qu’externes. L’évolution est donc plus ou moins rapide selon les contextes, mais elle donne finalement accès à un état d’équilibre : les deux variables-clefs, structures et fonctions, y varient de façon imprévisible car elles reflètent les variations aléatoires de l’environnement mais leurs moyennes restent constantes dans le temps. L’équilibre réalise ainsi un stade de maturité à complexité maximale, tel que l’activité normale se poursuit au meilleur niveau tant que rien d’inédit ne s’impose de l’extérieur. Pendant le temps d’accès à cet équilibre, le système est en outre susceptible d’avoir des échanges avec ses partenaires sous des modalités ordonnées ou non comme précisé plus loin.
Quant aux interactions de coalition, on est encore conduit à conjecturer qu’elles introduisent un ordre interne mais, pour le système complexe, le croisement des variables-clefs situe la coordination dans l’espace des fonctions. La coordination prend donc l’aspect de suites de fonctions se succédant selon un plan prédéfini, et qui est décrit par un paramètre d’ordre de niveau supérieur. Elle crée ainsi un comportement réglé à même de remplir un but apparent. Toutefois, la conjonction ordre-désordre découverte en physique se retrouve inchangée au croisement près : on conclut qu’un jeu de structures non-coordonné peut engager un comportement réglé unique. La biologie en fournit un exemple qui a longtemps posé un problème de principe (Blumenfeld 1981) : le code génétique se compose de bases chimiques qui se suivent sans coordination apparente (Dieter et al. 1994), et pourtant elles conduisent aux mêmes fonctions chez des individus identiques. C’est précisément la conjonction ordre-désordre qui trouve une explication immédiate dans la morphodynamique.
La théorie établit d’autres propriétés qui sont cruciales pour les systèmes très complexes du monde vivant. Premièrement, si plusieurs structures peuvent avoir des fonctions identiques, les plus performantes sont sélectionnées en priorité car elles sont les plus stables. Grâce à ce processus de sélection interne, les spécificités historiques de l’organisme peuvent engager l’évolution vers des spécialisations différenciées. Deuxièmement, les systèmes réels possèdent des fonctions multiples et complémentaires, et les paramètres d’ordre associés à ces fonctions peuvent interagir dans l’espace de configuration ; dès lors, l’interaction donne lieu à un ordre spatial de niveau supérieur, tel que formes d’organes ou structures composites. La procédure peut encore se répéter pour construire une hiérarchie à niveaux multiples alternant les paramètres d’ordre dans l’espace des fonctions et des structures. En combinant hiérarchisation et sélection interne, la morphodynamique peut donc rendre compte en principe des organisations les plus perfectionnées qu’on observe dans le monde vivant.
7. L’interprétation comportementaliste
La morphodynamique explique ainsi l’évolution du monde biologique dès sa naissance : elle rend compte de la croissance irréversible de la complexité des organismes par prolifération, diversification, différentiation ou spéciation ; elle rend compte aussi des ordres fonctionnels qui assurent les métabolismes à partir de codes génétiques non-ordonnés. Par sélection et hiérarchisation, elle rend enfin compte du développement des spécialisations et des coordinations sensori-motrices de haute performance.
Il en résulte une théorie de l’évolution biologique qui est plus complète que les théories néo-darwiniennes. En effet, celles-ci attribuent l’évolution vers les plus aptes aux mutations aléatoires et à la sélection naturelle ; or, ces mécanismes sont communs aux espèces, et donc peu propices aux grandes divergences qu’on observe à partir des ancêtres communs. A l’opposé, la sélection interne de la morphodynamique réhabilite les spécificités historiques des organismes qui poussent la performance ; la théorie rend ainsi intelligibles à la fois l’origine des plus aptes et l’apparence téléonomique de l’évolution.
8. L’interprétation cognitiviste
L’interprétation cognitiviste de la morphodynamique s’adresse aux systèmes mentaux. Elle les distingue formellement des autres systèmes biologiques par le fait qu’ils entretiennent des échanges prépondérants entre partenaires de complexité comparable : ces interactions au niveau système les amènent à organiser au niveau supérieur des sociétés qui stipulent leurs propres finalités.
Dans l’interprétation cognitiviste, la température complexe du système mental mesure le niveau de l’activité stochastique induite par les échanges aléatoires avec ses partenaires. Comme cette mesure tient compte de la performance des fonctions qui assurent les échanges, elle s’interprète comme le niveau de compétence dans le contexte socio-culturel. La suite de l’interprétation se fonde d’abord sur le croisement des variables pour identifier la nature des échanges, mais il convient de les comprendre ensuite dans la perspective de l’activité sociale spécifique des systèmes mentaux.
Selon la physique, la première modalité d’échange est le travail mécanique par lequel deux systèmes échangent des positions coordonnées de l’espace. Après croisement des variables, cette modalité implique qu’un système mental exécute des fonctions coordonnées au profit d’un partenaire : son comportement suit un plan fixe et reproductible, et il consiste à rendre un service préarrangé selon un savoir-faire. La première modalité représente donc la part prévisible et intentionnelle de l’activité mentale.
Quant à la deuxième modalité, la physique l’identifie comme la chaleur que deux systèmes échangent sous forme de quantités de mouvement désordonnées sans transfert de positions. Pour les systèmes mentaux, le croisement des variables implique que des valeurs de paramètres d’ordre non-ordonnées sont échangés sans exécution des fonctions associées. Visiblement, il s’agit d’un message fait de symboles en suites non-coordonnées et non-reproductibles. La deuxième modalité représente donc la part imprévisible et inventée de l’activité mentale.
L’originalité de la théorie est d’énoncer la première loi dynamique qui régit les deux modalités : elles sont transformables l’une dans l’autre et leur somme est conservée dans les transformations cycliques. En effet, la description est la transformation d’un savoir-faire en un message ; par contre, l’exécution est la transformation inverse d’un message en un savoir-faire. Ces transformations se pratiquent sans gain ni perte : la morphodynamique édicte ainsi le principe de conservation de la propriété qui est le pendant du principe de conservation de l’énergie en physique. Selon ce principe, les systèmes mentaux procèdent à des échanges équitables de diverses sortes : par exemple, le troc où l’on échange un travail ou son produit contre un autre produit, mais aussi l’achat où l’on échange un produit contre un message tel qu’un signe monétaire ; on peut enfin échanger des bien immatériels entre eux, comme un payement contre une information sensible, voire une marque affective. D’ailleurs, nous reconnaissons le principe de conservation dans la charte sociale qui condamne l’abus de confiance : qu’ils soient tangibles ou non, les biens échangés entre tiers doivent être équivalents pour que les contrats passés entre eux aient force légale, et les prix servent souvent à prouver l’équivalence.
Enfin, la théorie stipule la deuxième loi dynamique selon laquelle les interactions entre composants pourvoient à la complexification et à l’organisation hiérarchisée du système. Or, nous constatons que les personnes développent et réorientent leurs activités selon les services et les messages qu’elles ont échangés : ces échanges tiennent donc lieu des interactions qui déterminent les règles de comportement au niveau supra-individuel. La morphodynamique se mue alors en une théorie d’évolution sociale dans l’échelle du temps mental qui dépend des échanges interpersonnels : elle rend compte en parallèle de l’évolution culturelle et de la croissance économique par l’invention concordante de règles, de connaissances et d’artefacts. Par exemple, non seulement elle fait de la monnaie un moyen d’échange équitable, mais elle lui confère le rôle primordial de décompter les ressources que l’humanité peut consacrer à son effort de civilisation. Pour ce qui concerne l’activité mentale, la théorie reconnaît la nature particulière de ses produits, à savoir l’action intentionnelle et la représentation symbolique ; à ce titre, elle est à même de donner une nouvelle base épistémologique aux développements mentaux d’extrême complexité.
Cette perspective est par exemple prometteuse pour la formation du sens de soi et de l’autre en psychologie. En effet, à l’origine, le soi ne se distingue de l’autre que s’il sépare les expériences sensorielles provenant de l’intérieur et de l’extérieur : l’observation a montré que le critère clef est la prévisibilité des unes et l’imprévisibilité des autres (Stern 1985) ; or, selon les hypothèses de la morphodynamique, les échanges concourant à la complexification sont justement non-coordonnés. Ce critère est général car il assure que les représentations symboliques sont consonantes avec la réalité extérieure. On le reconnaît donc sans surprise parmi les critères d’objectivité des sciences exactes, garantissant par exemple qu’une théorie est objective si elle passe des tests imprévisibles lors de sa formulation (Robinson 1975). Une autre application prometteuse est l’émergence de la conscience comme le produit de l’interaction sociale par le langage (Humphrey 1984) et qui a une longue histoire (Jaynes 1976) : les personnages de l’Iliade ou de l’Ancien Testament ne sont pas conscients car ils sont mus par leur songes, et la volition comme faculté d’agir autonome n’apparaît dans la littérature que dans les époques troublées qui précèdent l’ère chrétienne ; la conscience individuelle et la maîtrise du destin personnel s’avèrent donc des conquêtes tardives et encore inachevées aujourd’hui.
9. L’émergence des significations
Le message est l’exemple familier de la coordination fonctionnelle imputable à l’interaction entre éléments structurels non-ordonnés. En effet, tout comme les bases du code génétique, les symboles d’un langage ne présentent pas de coordination entre eux (Dieter et al. 1994), mais le message porte normalement un sens bien déterminé. Or, les symboles ont des interactions répulsives et attractives spécifiées par les règles syntaxiques et sémantiques du langage, et le sens est saisi par une opération mentale non-rationnelle et quasi-instantanée qui exploite les dites règles. Par exemple, les deux vers qui suivent s’énoncent par les mêmes phonèmes, mais ils ont chacun un sens différent et sans autre relation que leur détermination mutuelle :
Gal, amant de la Reine, alla, tour magnanime,
Galamment de l’arène à la Tour Magne, à Nîmes.
Tant dans l’énoncé verbal que dans la version écrite, le flux continu des symboles indique la liaison grammaticale et sémantique, tandis que les coupures indiquent les appositions et les qualifications. Les différents sens des suites phonétiques n’émergent qu’à condition que ces interactions attractives et répulsives soient correctement signalées. On vérifie également que ces sens ressortissent à la narration d’un comportement complexe : la signification est contenue dans un paramètre d’ordre fonctionnel unique, mais il est lui-même porté par les éléments structurels multiples que sont les phonèmes.
Nous retrouvons donc à ce niveau abstrait la conjonction ordre-désordre déjà reconnue en physique et en biologie. Elle s’avère comme une propriété générale des langages. A la réflexion, elle paraît nécessaire pour qu’ils expriment des significations en nombre indéfini par le moyen d’ensembles symboliques finis : les arts comme la littérature ou la musique véhiculent en effet des significations innombrables au travers d’un petit nombre de symboles. La multiplicité repose sur l’emploi de règles d’interaction qui convertissent ces ensembles en systèmes symboliques. La définition de ces règles est l’affaire de la culture, rôle crucial reconnu depuis peu en psychologie culturelle (Bruner 1986) : la culture désigne les choses et les événements qui s’assortissent ou s’excluent, et elle distingue les enchaînements qui sont souhaitables ou inacceptables à un moment donné d’une civilisation (Illustration III : Message dont le sens dépend des interactions suggérées entre symboles peints et reconnues selon les règles culturelles en vigueur. Ici, confrontation de la réalité de l’habitat physique qui tend vers le désordre, et du rêve des habitants qui tend vers l’ordre. Selon l’auteur, un des messages possibles serait : “quand le mental ne met pas de limite, le physique va à vau-l’eau ; quand le physique ne met pas de limite, le mental glisse vers l’ordre et la volupté”). Ensuite, les aléas de l’histoire peuvent motiver des entorses aux règles sur lesquelles jugement est passé, et la culture évolue dans le temps socio-culturel.
10. Quelques interprétations pour la musique
Comme les autres arts, la musique est un langage à même de transmettre des contenus mentaux non-traitables par la langue parlée. Elle dispose d’un ensemble symbolique très riche : sons de timbres, durées, hauteurs et modulations diverses, liés ou séparés par des silences. La plus grande variété est possible mais les structures typiques des langages sont toutes présentes conformément à la morphodynamique.
Par exemple, la culture définit des relations syntaxiques et sémantiques, telles que règles de composition des rythmes, mélodies et harmonies, et règles de composition supérieures régissant les répétitions et les variations qui entrent dans une œuvre d’envergure. Ainsi, les symboles ont des interactions qui forment des paramètres d’ordre perçus comme des unités thématiques. Ces unités évoquent des états émotionnels ressentis comme induits de l’extérieur grâce aux variations imprévisibles qui accompagnent le thème, contrairement aux états spontanés qui sont prévisibles. Enfin, l’expérience de ces états constitue le sens du message ; comme le prévoit la morphodynamique, on constate que ce sens varie lorsque les auditeurs perçoivent les liaisons et les coupures différemment (Bamberger 1991).
La correspondance entre thèmes et états émotionnels évoqués fait l’objet d’une science à part, la musicologie : elle est l’analogue de l’éthologie qui étudie la correspondance entre configurations de signaux externes et comportements induits. Le sens d’un thème dépend du contexte qui précède et qui suit, et il peut être précisé ou approfondi par les variations. Thèmes et variations sont inventés dans une recherche incessante, puis sélectionnés empiriquement selon leur efficacité à transporter les significations émotionnelles recherchées. Cette recherche change la culture en renouvelant les règles admissibles pour la composition des messages musicaux.
Cependant, la théorie prévoit aussi que ces messages connaissent des limitations de fidélité. La première est que le message n’a pas toujours le même sens s’il passe entre émetteur et récepteur de niveaux de connaissance trop différents. La deuxième limitation est une asymétrie : s’il est toujours possible de traduire une intention en musique, il peut être difficile ou impossible d’y remonter à partir de la seule audition. Il en va de même avec le langage usuel : toute transformation par des symboles dégrade le contenu. Il est bien connu que nos paroles sont plus pauvres que nos pensées, et notre compréhension plus pauvre que les mots que nous entendons. On ne peut en faire l’économie : la fidélité requiert que l’émetteur et le récepteur puissent mobiliser les mêmes connaissances antérieures.
11. Conclusions
La musique est l’un des moyens de communication que les hommes ont inventés pour partager leurs émotions. Elle se montre structurée en un langage symbolique comme le requiert la morphodynamique des systèmes complexes. Cette théorie explique en principe l’ascension continue des êtres vivants vers la complexité : en rendant finalement l’humanité capable d’inventer des langages dans le temps mental, l’évolution biologique se perpétue aujourd’hui sous la forme socio-culturelle, et la spéciation fait place à la signification. Par ce biais, la morphodynamique rend intelligible le pouvoir que la musique possède de transmettre des messages que nous comprenons. Qualifié de “scandale intellectuel permanent” dans l’introduction à ce colloque, ce pouvoir garde toutefois son mystère car la théorie laisse intacte l’aura irrationnelle entourant tout acte de création.
Appendice : Dynamique des systèmes
La dynamique des systèmes est la théorie qui décrit les changements observés dans les systèmes considérés comme ensembles de composants. Elle définit opérationnellement les variables appropriées aux composants, y compris le temps, et établit les équations qui relient ces variables ; enfin, elle déduit les lois des systèmes en combinant les équations de tous les composants. Ces opérations sont résumées ci-dessous pour les systèmes physiques et les systèmes complexes : il en ressort que leurs dynamiques sont isomorphes bien qu’elles se distinguent par le croisement des variables de configuration et de flux.
1. Systèmes physiques
Les composants sont des particules de masse m, pour lesquelles la dynamique à une dimension prévoit la position x en fonction du temps t suivant la force appliquée F. L’observation montre qu’une variable intermédiaire varie aussi dans le temps, la quantité de mouvement p ; rapportée au volume, elle représente plus précisément un flux temporel de matière, soit la quantité de matière traversant une surface unité en un temps unité. Sur la base de notre intuition du temps s’écoulant spontanément, on conjecture que les variables obéissent aux équations de Newton :
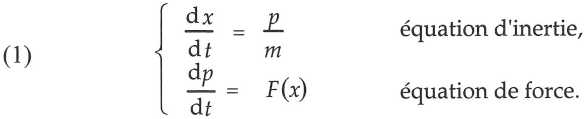
Avec la force attractive et linéaire F (x) = – k x, les équations ont une solution périodique qui est vérifiée par l’expérience. A ce point, on conclut que les conjectures faites sont justes : les variables dynamiques conjuguées x et p, la force F et la variable temps t sont quatre grandeurs a priori indépendantes mais codéterminées opérationnellement par l’intermédiaire des équations dynamiques.
2. Systèmes complexes
Les composants sont des structures fonctionnelles qui transitent entre deux états stables et produisent une fonction particulière à des taux nettement différents dans chaque état. Ces structures sont conditionnellement adaptatives : suivant leur état interne, elles restent fixes ou transitent à un certain seuil d’une influence externe ; la transition a alors a pour effet de changer le taux de production de la fonction associée suivant l’état de l’environnement. La dynamique a pour but de décrire le débit fonctionnel en fonction d’un temps approprié. Selon ces descriptions, la première variable x est celle qui repère l’état momentané du composant, c’est-à-dire le paramètre d’ordre d’un système physique à dynamique de bifurcation soumis à l’influence externe I ; la deuxième variable est le débit fonctionnel p dans l’état repéré par x, c’est-à-dire la quantité d’énergie-matière traitée par unité du temps. Les équations dynamiques couplées suivantes satisfont les conditions énoncées :
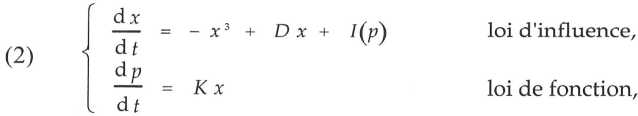
avec D et K des constantes caractéristiques du composant. Dans cette dynamique unidimensionnelle, la structure change d’état selon la valeur de la constante D : si D est négatif, la variable de configuration x reste pratiquement invariante, mais si D est positif, elle transite entre ses deux déterminations stables lorsque le paramètre I (p) atteint des valeurs critiques. D représente donc le seuil de sensibilité de la structure à l’influence extérieure I. La deuxième équation affirme que, après la transition de x, la fonction associée p croît dans le temps au taux caractérisé par K, constante définie positive qui évalue le niveau de performance de la structure. Les deux équations représentent donc bien la propriété d’adaptation conditionnelle des structures fonctionnelles, et il apparaît que les constantes D et K caractérisent un composant de l’appareil sensori-moteur d’un système vivant.
Comme en physique, ces équations dynamiques sont initialement des conjectures. Avec l’influence attractive et linéaire I (p) = – v p, les équations ont une solution périodique qui est vérifiée par l’expérience. A ce point, on conclut que les conjectures sont justes : les variables dynamiques conjuguées x et p, l’influence I et la variable temps t sont identifiées comme quatre grandeurs a priori indépendantes mais codéterminées opérationnellement par l’intermédiaire des équations dynamiques.
3. Comparaison des dynamiques
En conséquence, on voit le temps revêtir la même signification générale du point de vue opérationnel, à savoir le rapport existant entre les variables observables de configuration et de flux. Explicitement, les Éq. (1) et (2) définissent l’accroissement de temps dans les systèmes physiques et complexes respectivement par :

On constate que les rôles dynamiques des variables de configuration et de flux sont croisés ; en outre, selon les Éq. (1), les positions sont continues et les quantités de mouvement éventuellement discontinues en physique, alors que selon les Éq. (2), les flux sont continus et les variables de configuration sont éventuellement discontinues dans les systèmes complexes. Visiblement, ces grandeurs ont entre les deux types de systèmes des différences de nature irréductibles qui disqualifient toute analogie directe entre eux. Toutefois, les relations mathématiques ont la même structure : l’isomorphisme formel est établi entre les deux dynamiques et le seul changement concerne les interprétations des variables.
4. Passage aux systèmes
Les systèmes physiques fermés sont formés d’un grand nombre de particules se mouvant dans l’espace à trois dimensions, dénombrées par l’indice i, i = 1, …, N, d’où le système de 2N équations :
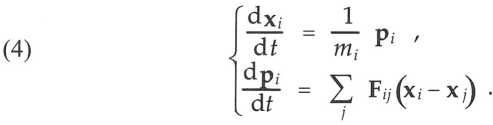
Le chaos produit par les interactions Fij justifie l’hypothèse ergodique selon laquelle les variables évoluent en moyenne temporelle vers leur moyenne spatiale sur toutes les particules ; avec les crochets représentant cette prise de moyenne, le système accède à l’état d’équilibre thermodynamique caractérisé par la température :
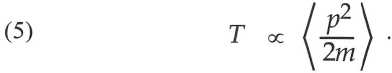
De leur côté, les systèmes complexes comptent un grand nombre de structures fonctionnelles qui interagissent par l’intermédiaire de leurs flux ; en outre, le couplage à l’environnement réel leur impose des influences externes qui sont constantes à court terme, mais elles peuvent varier tout en restant incoordonnées à moyen et long terme. Le système formé de N structures d’indice i, i = 1, …, N, est alors décrit par le système de 2N équations :
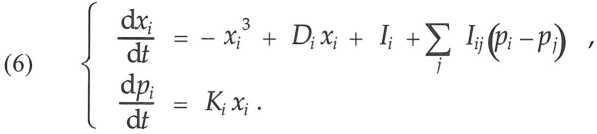
Comme les variables sont unidimensionnelles, les interactions mutuelles Iij ne produisent pas le chaos endogène trouvé dans le cas tridimensionnel de la physique. En revanche, le terme d’influence externe Ii est aléatoire et constitue la source de chaos exogène conférant un comportement chaotique aux variables microscopiques. Ce comportement est donc analogue à l’agitation thermique régnant dans les systèmes thermodynamiques, et il justifie que l’hypothèse ergodique s’applique avec les mêmes conséquences macroscopiques : les systèmes complexes subissent une évolution nécessaire vers un état d’équilibre à long terme. Cet équilibre morphodynamique se caractérise par une variable macroscopique calculée par prise de moyenne sur tous les composants et appelée température complexe :
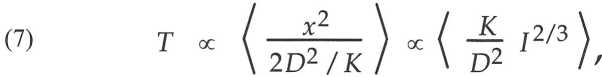
le dernier résultat provenant de la dynamique de bifurcation sous influence externe. En conclusion, l’hypothèse ergodique s’applique de manière identique dans les deux types de systèmes de sorte qu’ils présentent un isomorphisme complet entre les grandeurs et relations de nature statistique. Les lois macroscopiques sont donc identiques dans les deux théories, thermodynamique et morphodynamique, mais les mécanismes conduisant à l’équilibre sont totalement différents, de même que les interprétations des grandeurs concernées.
Références
Bamberger, J. (1991), The Mind Behind the Musical Ear. Cambridge, (Mass.), Harvard University Press.
Blumenfeld, L. A. (1981), Problems of Biological Physics. Berlin, Springer, p. 14.
Boulding, K. E. (1981), Evolutionary Economics. London, Sage.
Bruner, J. (1986), Actual Minds, Possible Worlds. Cambridge (Mass.), Harvard University Press.
Dawkins, R. (1991), The Blind Watchmaker. London, Penguin Books.
Dieter, G. and Zhang, Y. (1994), « Crossover from White Noise to Long-range Correlated Noise in DNA Sequences and Writings », Fractals, 2, 4, 473-479.
Edelman, G. M. (1987), Neural Darwinism. New York, Basic Books.
Humphrey, N. (1984), Consciousness Regained. Oxford, Oxford University Press.
Jaynes, J. (1976), The Origin of Consciousness in the Breakdown of the Bicameral Mind. Boston, Houghton Mifflin, p. 447.
Robinson, H. J. (1975), Renascent Rationalism. Rockwood, Speedside, chap. 5.
Stern, D. (1985), The Interpersonal World of the Infant. New York, Basic Books, chap. 4-5.
Winfree, A. T. (1987), The Timing of Biological Clocks. New York, Scientific American Library, Freeman & Co.
Zeeman, E. C. (1972), « Differential Equations for the Heart Beat and Nerve Impulse », in Towards a Theoretical Biology. Ed. C. H. Waddington, Edinburgh, University Press, vol 4, 8-67.