Faute de documents suffisamment explicites, la reconstruction de la théorie musicale grecque avant Aristoxène de Tarente repose souvent sur des bases conjecturales. On sait cependant que l’étude de l’harmonie n’est pas une prérogative de la théorie musicale au sens strict. Les premières réflexions dans ce domaine se développent dans le cadre d’un concept particulier de musique qui est le fruit d’un parallélisme étroit établi entre l’harmonie et toute une constellation de disciplines complémentaires gravitant dans son orbite périphérique : physique des éléments, physiologie humorale, théorie des proportions, cosmogonie. A la base de ce concept une définition particulière du langage musical réduit toute musique à une harmonie de contraires : qu’elle se déploie dans la durée ou dans les hauteurs, l’harmonie est un mixte d’éléments (stoicheia) antagonistes – unités, relations de nombres pairs et impairs, sons aigus, graves, intervalles de toutes sortes, tétracordes différents selon le genre, tons de transposition, syllabes longues, brèves ; le tout articulé en un système organique hiérarchisé, simple au sommet et complexe à la base. Incontournable, l’idée d’un rapport mimétique reliant l’harmonie sonore à l’harmonie des éléments en conflit dans les corps physiques conduit alors la pensée à intégrer dans les compétences de la théorie musicale des domaines aussi divers que la mélodie, la composition d’un médicament, le mélange du vin et de l’eau dans le cratère, l’anthropométrie d’une statue, la façade d’un édifice, le rythme des saisons, les jours 6 : 8 : 9 : 12 de la grossesse, le développement harmonieux de l’embryon, le rapport entre systole et diastole, le concert des qualités humorales dans le tempérament, l’équilibre des états d’âme, le paroxysme fébrile, les révolutions astrales, la roue des naissances et même le retour cyclique de l’histoire. La musique est alors langage sonore mais aussi science du rapport logique, préparation à la dialectique, episteme, issue d’une pensée qui se connaît elle-même en miroir, qui prend conscience de soi en contemplant son image réfléchie dans l’univers des formes qu’elle produit. De là l’idée d’un champ d’investigation débordant le cadre étroit de la théorie musicale “proprement dite”.

Faut-il se servir d’Aristoxène pour comprendre la métrique de la poésie d’Alcman, de Simonide, de Pindare et des tragiques ? A la fin du siècle passé la plupart des métriciens partagent cet avis, de Boeckh à Gevaert en passant par Westphal.

Tant que les écrits métriques des grammairiens de l’époque romaine formaient la source unique de nos connaissances en tout ce qui concerne le rythme antique, il était difficile de voir dans les restes les plus distingués de la littérature mélique autre chose que des textes ayant servi à une musique bizarre, étrangère à toute mesure régulière et plus destituée d’eurythmie que les chants des peuplades sauvages. Une intelligence suffisante de la rythmique d’Aristoxène a montré que les Grecs, cette noble race si éprise d’ordre et d’harmonie, ne se sont pas mis en dehors des lois de la nature, ce que d’ailleurs les philologues auraient pu soupçonner a priori (Gevaert, II, 69-70).

D’importantes réserves quant à cette éventualité figurent chez Wilamowitz-Moellendorff (1921), qui a souligné le caractère fourvoyant de cette théorie pour l’intelligence de la métrique antique. Depuis, ses conclusions ont reçu le suffrage de la plupart des auteurs modernes.

L’autorité d’Aristoxène pour la compréhension du système des hauteurs – un domaine que la théorie antique ne sépare pas de celui de la durée – n’est guère moins controversée. Le musicologue allemand Johannes Lohmann déclare :

La réalité proprement dite dans la musique grecque est le système des tonoi […] ce système […] n’est pas toutefois, contrairement à ce que pense Gombosi, un système de transposition ; c’est un système de position, dans lequel seulement les valeurs abstraites idéales des niveaux de tons (idynameis) sont mises en position. Le tonos au sens technique constitue la réalité musicale proprement dite, et cela dès le début (Lohmann, p. 72).

Cette interprétation contredit ouvertement les thèses en vigueur dans les pays anglo-saxons. A. Barker a fait sienne l’idée de Winnington-Ingram suivant laquelle les harmoniai décrites par les auteurs de la fin du cinquième siècle n’auraient rien en commun avec les éléments d’un système de hauteurs relatives (tonoi) en élévation progressive à l’intérieur de l’octave.

Les harmoniai ne se distinguent pas en raison de leur emplacement dans les différentes régions du registre, et leurs différences n’ont rien à voir avec la hauteur relative de l’exécution ; bien que la terminologie soit risquée, on peut affirmer qu’une harmonia s’apparente bien plus à un mode qu’à une tonalité¹ (Greek Mus. Writings, II, 17ss.).

Le conflit entre tonoi n’aurait joué un rôle syntaxique que dans l’intervalle qui sépare la République de Platon des Eléments d’Aristoxène.

Mais il apparaît assez clairement que les harmoniai de la fin du cinquième et du début du quatrième siècle […] se distinguaient les unes des autres avant tout en vertu d’une succession différente des intervalles. Il existe, il est vrai, assez de témoignages provenant d’époques différentes suivant lesquels chaque harmonia se trouvait associée à un registre particulier, certaines étant regardées comme aiguës, d’autres comme graves, […] et sans aucun doute ce fait aida l’attribution des différents caractères auxquels font allusion nos sources. Mais les premières analyses techniques dont nous avons connaissance ne prêtent que peu d’attention à ce phénomène, et distinguent les harmoniai presque exclusivement par la structure d’intervalles qu’elles affichent. […] A une date probablement peu éloignée de celle de la République, les théoriciens s’engagent dans le projet de ranger les structures des harmoniai existantes dans le cadre d’un système intégré unitaire. C’est à ce système que font allusion de nombreuses sources postérieures, et nous ignorons combien il était artificiel, avec quel respect ou quelle désinvolture il traitait les problèmes de l’exécution proprement dite. Nous ne savons pas non plus si ce système, sous cette forme, était familier à Platon² (Greek Mus. Writings, II, 17ss).

L’état de la syntaxe musicale à l’aube de l’ère hellénistique paraît moins problématique. Le lexique des Eléments d’Aristoxène mentionne aussi bien les tonoi que les espèces d’octave. Le terme eidos, forme, aspect [d’octave], désigne le nombre complet de toutes les permutations subies par les intervalles enfermés dans un ambitus donné, de quarte, de quinte ou d’octave. La notion du tonos, en revanche, est étroitement liée au concept aristotélicien de puissance. Toutes les quartes, dans la succession descendante de quartes la-mi/ sol-rél/ fa-do, présentent une dimension identique. Dans chaque forme, toutefois, chaque note assume une valeur ou fonction (dynamis) spécifique déterminée par le contexte ou la forme dans laquelle elle s’insère (puissance, valeur, fonction tonale). La fonction d’un intervalle se révèle indépendante de la hauteur et étroitement liée au contexte qui l’entoure : on peut générer toutes les formes d’une consonance en faisant glisser ses extrêmes dans un sens ou dans un autre sur une échelle donnée et en même temps obtenir le même résultat en modifiant, par des “altérations”, son agencement interne sans déplacer ses bornes. On s’aperçoit dès lors que les trois quartes la-mi, sol-ré, fa-do existent en puissance dans les valeurs la-sol-fa-mi, la-sol-fa#-mi, la-sol#-fa#-mi ; ou, si l’on préfère, dans trois tonoi placés à trois hauteurs différentes. Le passage d’un tonos à l’autre – conçu en tant qu’actualisation des puissances d’un substrat commun – est alors possible en vertu de l’ambiguïté établie par deux notes de même valeur mais de hauteur différente ; par exemple en passant du tonos Dorien au tonos Phrygien par la note si, qui est à la fois paramese katadynamin du Dorien et mese katadynamin en Phrygien. L’état fragmentaire des sources laisse cependant la question de la valeur tonale ou modale des harmoniai sans réponse. Une des thèses les plus courantes sur ce point accorde à Aristoxène le mérite d’avoir élaboré le premier un système général de tonalités offrant un dénominateur commun à toutes les mesai des modes³.

La question fondamentale, dans toute cette discussion, consiste à déterminer le critère de différenciation en vertu duquel un rythme ou une configuration de foyers mélodiques s’écarte de l’universalité incolore pour assumer, suite à une altération, un caractère spécifique. Cette difficulté en suppose une autre, relative au degré de complexité atteint par le système harmonique à sa rupture. Il s’agit de savoir si le principe d’individuation des qualités d’un mode d’une harmonia ou d’une forme rythmique concerne exclusivement le plan strictement élémentaire du système, comme la qualité des notes et des mètres en soi, ou bien la relation établie par ses éléments constitutifs dans ses ramifications formelles plus abstraites, comme la permutation cyclique des mêmes intervalles à l’intérieur de l’octave, la fonction ou puissance (dynamis) des notes dans le contexte d’un réseau particulier de rapports harmoniques.

La question des durées pose des difficultés essentiellement analogues. Est-ce le plan des composantes élémentaires d’une structure temporelle – la syllabe – qui détermine la signification d’une succession métrique, ou bien le cadre rigide des relations qu’on lui impose de l’extérieur qui détermine une conception abstraite de la forme ? Est-ce la présence ou l’absence d’une mesure caractéristique – péon, dochmiaque, dactyle, trochée – ou bien la permutation des parties – dactyle-anapeste, dipodie-tripodie, métabole rythmique – à l’intérieur des mesures qui détermine la qualité d’une structure rythmique ? La syllabe est-elle une mesure fixe, ou bien un substrat passif, sujet à un nombre infini de déterminations formelles ? Les syllabes sont-elles longues ou brèves en soi ? Est-ce au niveau de la matière ou de la forme que s’opère l’individuation de la qualité spécifique (ethos) d’une structure musicale ?

Toutes ces questions conduisent à des solutions différentes selon l’attitude de la pensée à l’égard du changement qualitatif. On sait par exemple que les principales catégories mentales sur lesquelles s’édifie la philosophie des systèmes d’Aristoxène – dynamis, dialectique puissance-acte, dichotomie forme-matière, théorie des métaboles – supposent les réflexions d’Aristote sur la philosophie de la forme et de ses transformations. Ainsi, une méthode légitime pour tenter de mesurer la distance qui sépare la théorie d’Aristoxène de celle de ses prédécesseurs consiste à interroger les sources sur les catégories mentales engagées dans l’analyse de l’altération qualitative des formes harmoniques : un chapitre bien connu dans l’histoire de la physique.

En dépit de leur caractère lacunaire, les écrits d’Aristoxène offrent à la plupart de ces interrogations des réponses nonambiguës. Dans les Fragmenta rythmica, l’ouvrage de référence à l’époque hellénistique⁴, Aristoxène fait sienne la vue traditionnelle suivant laquelle l’organisation de la durée, comme celle de la mélodie, est un système d’éléments simples agglomérés en structures syntaxiques complexes, selon un processus d’abstraction croissante, dont on trouve des traces dans la subdivision interne des études rythmiques en cinq parties : étude du temps premier, genres de mesures, allure rythmique (agoge), métaboles (metabolai), rythmopée ou composition rythmique. L’apport d’Aristoxène à l’enseignement traditionnel de la métrique réside avant tout dans la séparation de deux plans jusque là confondus. Largement tributaire des catégories élaborées par son maître Aristote, Aristoxène distingue le rythme (rythmos) du rythmé (rythmizomenon), le rythme en tant que forme abstraite (schema) de la matière passive qui lui sert de substrat (hypokeimenon). « Ils sont l’un à l’autre ce que la forme est à ce qui revêt une forme » (Gevaert, II, 9). A son état brut, la matière du rythme est une substance passive indéterminée et continue du point de vue géométrique. Elle est à la durée ce que le mouvement indéterminé de la voix est à la hauteur. De l’infini, toutefois, il n’y a pas de science : contrairement au rythme, le rythmé se laisse appliquer à toutes sortes de mesures et à toutes les combinaisons de temps. Il ne devient langage qu’au moment où la présence d’une limite discrète crée la possibilité d’une unité de mesure qui puisse assurer la commensuration de tous les niveaux hiérarchiques du système. D’où la célèbre définition aristoxénienne du temps premier (chronos protos), unité isochrone, qui est au rythme ce que le son – comme stase du mouvement topique de la voix indéterminée – est au système harmonique (Aristoxène, Komm, 4, 78-9 ; cf. Aristoxène, Elem. ryth., p. 32ss). Le rythme est alors rapport logique et discours, selon la double étymologie du mot logos : la disposition variable des temps premiers crée la forme (schema), qui résulte « d’une certaine disposition des parties de la matière » (cité par Gevaert, II, 9). Et la succession des formes dans la durée organisée crée le sens.

Cette forme est perçue comme quelque chose de plus qu’une simple organisation de la durée. Le schéma rythmique est à la succession des temps premiers ce que le nombre est aux unités de la série arithmétique : une physionomie reconnaissable dans la masse anonyme des unités sans identité, des individus sans nombre, qui ne comptent pas, selon une expression consacrée par Pindare. Le tissu de relations définies par le devenir de ces formes en évolution dans le temps est l’expression d’une pensée pure devenue configuration sémantique, voire même qualité et caractère. A preuve, la présence, dans le programme des études rythmiques, d’une section ad hoc consacrée à l’altération (alloiosis) qualitative des rythmes. Il s’agit, on le sait, d’un terme technique consacré par les catégories aristotéliciennes, qu’Aristoxène emploie dans toute son acception technique. Il désigne le mouvement (kinesis) dans la catégorie de la qualité, qui constitue, avec la génération et la corruption, l’une des trois espèces du changement (metabole). Alors que la génération (genesis aplos) opère une transformation générale du substrat en quelque chose de fondamentalement différent, l’altération limite son action aux seules qualités accidentelles.

Du moment qu’il y a d’un côté la réalité du sujet et d’un autre côté l’affection (pathos), il y a altération quand le sujet restant identique et perceptible, un corps ou un être change dans ses affections, que celles-ci soient contraires ou intermédiaires ; ainsi l’airain est tantôt rond tantôt anguleux et le corps est tour à tour bien portant et malade (Aristote, De generatione, 319 b 10).

Aristoxène est probablement le premier théoricien de la musique à consacrer un chapitre spécifique à cette notion. On en trouve des traces, à propos des hauteurs, dans le traité d’harmonique : « J’entends par métabole toute modification accidentelle (pathos) produite dans l’ordre de la mélodie » (Aristoxène, Elem. Harm., p. 47). Cette transformation est en réalité une altération puisque la transformation des échelles s’applique à un substrat sonore passif, c’est-à-dire le système parfait non-altéré du tonos dorien⁵, qui est à l’harmonie ce que le rythmizomenon est à la durée. Aristoxène qualifie d’altérations les modifications produites dans le tétracorde par la distribution variable des notes mobiles – modifications qui différencient les tétracordes en trois genre s – diatonique, chromatique, enharmonique. Le même concept désigne également la qualité modale – dorienne, phrygienne, lydienne – définie dans le tétracorde par la permutation cyclique des intervalles à l’intérieur des notes fixes⁶ (Aristoxène, Elem. Harm., p. 50). Dans un cas comme dans l’autre, la modification concerne les accidents d’un substrat qui, restant “identique et perceptible”, oscille dans la catégorie de ses affections ou qualités affectives. La qualité d’une échelle ou d’un rythme se confond alors avec la relation et la disposition variable des mêmes éléments et non l’objet de cette modification. L’énoncé d’Aristide Quintilien ne laisse aucun doute à cet égard : « la métabole est une altération (alloiosis) du système qui sert de substrat (hypokeimenon) et du caractère (ethos) de la voix » (Aristide Quintilien, De Mus., I, 11, 22 ; cf. Greek Mus. Writings, II, 424). Dans le système aristoxénien, cette dichotomie en suppose une autre, également inspirée des catégories de la pensée aristotéliciennes : la distinction entre la valeur des notes contenue en puissance (dynamis) dans les systèmes (tonoi) en élévation dans le registre et leur hauteur actuelle (thesis). Cette distinction permet d’affirmer que la même échelle peut changer qualitativement sur le plan dynamique (dynamis) tout en restant la même du point de vue de sa position (thesis) dans le registre. En transposant la définition aristotélicienne de l’altération en termes de hauteurs, on peut affirmer qu’il y a altération des échelles quand, le système parfait sous-jacent restant identique et perceptible, une harmonie subit une transformation dans la catégorie de ses affections contraires, aiguës ou graves du point de vue dynamique ; ainsi la même échelle est tantôt dorienne, tantôt phrygienne, tantôt “aiguë”, tantôt “grave” tout en demeurant la même du point de vue thétique. Le système hellénistique des tonoi n’est autre qu’une application de ce principe philosophique.

L’indication plus précise quant au corrélatif rythmique de ce phénomène – que l’état lacunaire des Fragments rythmiques laisse à l’état d’un simple sous-entendu – figure dans le traité d’Aristide Quintilien : « la métabole rythmique est une altération (alloiosis) des mesures et du mouvement (agoge) » (Aristide Quintilien, De Mus., I, 19, 40 ; cf. Greek Mus. Writings, II, 444). On peut modifier le tempo (agoge), le rapport des mesures, la disposition différente des temps à l’intérieur de la mesure, le changement du rapport rythmique des pieds ; on peut passer d’un rythme composé à un autre rythme composé, d’un rythme non composé à un rythme composé, d’un rythme irrationnel à un rythme rationnel et vice-versa. Cette formulation suppose une conception de la forme qu’Aristide n’a pas pu trouver ailleurs que dans un emprunt, direct ou indirect, des Fragments rythmiques d’Aristoxène (Aristoxène, Elem. ryth., p. xlvi) :

Ainsi que la matière affecte plusieurs formes, selon que toutes ses parties ou quelques-unes d’entre elles sont diversement disposées, de même chacune des matières propres à recevoir le rythme [à savoir le son, la parole et le geste] prendra diverses formes [rythmiques] non en vertu de sa nature propre, mais en vertu des propriétés inhérentes au rythme. En effet, un seul et même texte poétique, étant réparti en des temps rythmiques différents, donnera lieu à des variétés provenant de la nature du rythme lui-même. Il en est de même pour la succession mélodique, et en général pour tout ce qui est mesurable au moyen d’un rythme constitué par des temps [isochrones, c’est-à-dire par une unité fondamentale] (Gevaert, I, 9).

Faut-il projeter les éléments de cette doctrine dans le passé lointain du cinquième et du sixième siècle avant J.-C. ? Un moyen de répondre à cette interrogation est une archéologie des modèles logiques en matière de changement, dont l’histoire a évolué en syntonie avec les étapes de la physique présocratique. La première difficulté à laquelle se heurte la reconstruction toutefois pose quelques problèmes d’ordre philologique, qu’il convient de résoudre par un mouvement de va-et-vient entre modèles mentaux archaïques et ceux de la pensée qui les a véhiculés en les déformant. Aristote n’a pas hésité pas à faire l’honneur de sa propre doctrine de l’altération à Thalès et à la plupart des “monistes” présocratiques. Tous les naturalistes convaincus que l’univers est “une certaine unité” auraient ramené la variété du monde physique aux altérations d’une même substance primordiale éternellement identique à elle-même mais différente quant à ses accidents. Or, une brève réflexion sur les modèles logiques que suppose cette formulation permet de montrer l’anachronisme de cette hypothèse. La mécanique aristotélicienne de l’altération suppose une définition très rigide de l’opposition identité-diversité ainsi qu’une distinction nette entre les catégories de l’essence et des accidents. Or, si l’anti-thèse identité-diversité trouve sa première formulation rigoureuse dans le contexte de la dialectique éléate, la dichotomie essence-accident paraît impensable avant les recherches logiques inaugurées par Platon sur les traces de Socrate. En outre, l’oscillation entre couples de qualités contraires dont il est question dans la théorie aristotélicienne de l’altération suppose le théorème de la dichotomie à l’infini, que Zénon est le premier à formuler avec précision. Il suit de là que la conception présocratique du temps et de la forme devait répondre à des critères aux antipodes des catégories de la rythmique d’Aristoxène ; et on comprend l’attitude polémique d’Aristoxène à l’égard de ses prédécesseurs.

Démocrite a écrit deux ouvrages perdus sur l’harmonie et sur le rythme. Il n’en reste que les titres. Cependant, ses opinions en matière de changement qualitatif sont bien connues. Les atomes sont immuables du point de vue qualitatif. L’hypothèse d’un substrat identique et perceptible en oscillation dans la catégorie des accidents paraît exclue. L’altération est une génération et le changement est le fruit d’un art combinatoire réalisé en permutant la distribution d’atomes de même qualité. L’impossibilité de concevoir des atomes de qualité différente pour le feu, l’air, la terre, l’aigu et le grave conduit le philosophe à placer la variété des qualités dans la forme (rythmos), l’ordre, le groupement (diatige) et l’orientation dans l’espace (trope) des atomes. Toute conclusion quant aux éventuelles conséquences musicales de ces doctrines paraît téméraire. Une chose cependant est certaine. L’idée d’une doctrine isolant la puissance des notes et des rythmes de leur substrat réel (acuité et durée de la syllabe), dans ces conditions, paraît aussi improbable que la doctrine de l’altération. De plus, les idées de Démocrite en matière de devenir enferment en puissance l’idée d’une conception modale de la variété. Dans la mesure où le changement est une permutation d’éléments identiques, l’aigu et le grave supposent une différence de densité ; un mode diffère de l’autre en vertu de la permutation cyclique de ses intervalles à l’intérieur de ses deux extrêmes et le caractère des pieds métriques se transforme en fonction des modifications imparties à l’ordre des syllabes longues et brèves à l’intérieur de la mesure.

Cette doctrine qui place la qualité dans la relation et non dans les éléments n’aurait probablement pas vu le jour à cette date si les Éléates n’avaient pas exclu, sur la base de réflexions sur la continuité de l’espace, la possibilité même du devenir. Le théorème de la dichotomie à l’infini divulgué vers 470 dans les paradoxes de Zénon exerça une influence d’une portée extraordinaire sur l’histoire de la physique. Il enseigna à concevoir le changement qualitatif dans l’abstrait, sous la forme d’un mouvement oscillatoire parcourant une ligne géométrique divisible à l’infini. La qualité des mixtes pouvait apparaître comme un attribut abstrait et séparé de son sujet.

Avant cette date, l’être n’exclut pas le devenir et la physique ignore aussi bien l’idée d’une qualité accidentelle que celle d’une séparation des formes de leur “substrat”. On connaît, grâce aux opinions conservées par Aristote dans la Métaphysique, le point de vue très instructif des pythagoriciens du V^e siècle quant à l’immanence des principes numériques du monde. Plutôt que ramener la multiplicité du monde physique à l’air ou au feu, les philosophes de l’école italique réduisent cette variété à un système d’éléments numériques pairs et impairs mêlés en proportions variables dans tous les êtres. Ils considèrent que les principes des nombres sont les éléments de tous les êtres et que le ciel tout entier est harmonie et nombre. Or, l’unité qui compose les nombres est un corps physique. La génération de la durée et de l’espace suppose une agglomération d’unités discrètes pourvues d’une dimension spatiale et soumises, d’une manière générale, à toutes les affections des corps physiques : pesanteur, densité, raréfaction, température (Aristote, Métaphysique, 1090 a 30ss). L’unité est, à la fois, un corpuscule et le principe – identique à l’Impair – qui maintient les choses dans leur propension obstinée à persévérer en ce qu’elles sont. Le Pair est le corrélatif mathématique de l’air et de l’indéterminé (apeiron). Le pair exerce une action déformante : il pénètre parmi les interstices des unités à la façon d’un souffle, créant des excroissances qui entraînent les corps des systèmes à se diviser par dichotomie, ou par mitose. La disposition des unités en configurations géométriques sur le sable – suivant laquelle l’addition des nombres impairs produit la série des nombres carrés (1 + 3 = 4 = 2x2 ou 2 : 2, 1 + 3 + 5 = 9, 1 + 3 + 5 + 7 = 16) – montre que l’Impair confère aux formes l’Identité. L’addition des nombres pairs (2 + 4 = 6 = 3x2…), qui produit une série de rectangles modulant sans cesse les rapports de leurs côtés, conduit les formes à franchir le cadre de leurs limites. Le monde est un mixte de pair et d’impair. Si le pouvoir centripète de l’un n’était pas contrecarré par la vertu déformante du pair, l’harmonie du monde se réduirait à un interminable unisson. Livré à la domination du pair, elle se transformerait en une chimère difforme, analogue aux bovidés à face d’homme enfantés, sous le ciel de la Haine, dans l’imagination d’Empédocle.

Formes, matières, qualités, substances, accidents, mouvement et devenir se confondent dans le même principe numérique. D’où la présence, au cœur du dispositif, d’un certain nombre d’archaïsmes prélogiques, telle cette idée suivant laquelle le nombre se composerait d’éléments numériques pairs et impairs, qui conduit à imaginer le nombre à la fois comme principe formel et élément de ce même principe. C’est dans ce sens qu’il convient de comprendre le témoignage d’Aristote suivant lequel le nombre est principe à la fois comme cause matérielle des êtres et comme cause efficiente de toutes leurs transformations (Aristote, Métaphysique, 986 a 15). Cette affirmation exclut l’hypothèse d’une divinité qui créerait le monde en lui imposant une forme harmonique de l’extérieur, comme le démiurge du Timée platonicien. Le nombre est à la fois table et ouvrier ; il est bois, mais il contient en son germe les principes mêmes de sa transformation en une table. D’où l’idée d’un monde animé par le nombre. L’univers pythagoricien respire au rythme du temps et des saisons et s’accroît suivant des mécanismes embryologiques. Le nombre est graine, cellule, semence (Aristote, Métaphysique, 1091 a 14ss). L’auteur d’un fragment pythagoricien conservé dans le traité pseudo-hippocratique du Régime conçoit la croissance de l’embryon sous la forme d’une génération harmonique. Des particules numériques sexuellement contraires, paires et impaires, se mêlent dans la matrice pour enfanter une unité “diploïde” complexe enfermant en son sein l’être tout entier. Lorsque son cœur commence à battre, elle commence à respirer. Rendue turgescente par l’air qui l’entoure, elle se divise en deux, puis en trois et en quatre, suivant la proportion des intervalles musicaux de quinte, de quarte et d’octave. Pair et indéterminé, l’air inhalé par la matrice sculpte le corps de l’embryon dans toutes les directions, freiné par la puissance modératrice de l’impair. Lorsque les particules se disposent de manière inharmonique, le nouveau-né est difforme. Une indication précise, dans la Métaphysique d’Aristote, conserve les traces d’une cosmogonie conçue en termes strictement analogues. Limite et Illimité s’accouplent en une hiérogamie cosmique quelque part dans la matrice de l’univers et enfantent une première unité androgyne – pair-impair – qui contient en germe le monde. Le cœur de celle-ci commence à battre et à inhaler l’air indéterminé qui l’entoure. Puis elle gonfle sous l’impulsion déformante du pair ; ensuite elle se dédouble, elle génère le triple, le quadruple, la quinte, la quarte, l’octave et l’ensemble des mixtes de l’univers physique. L’idée d’une séparation des formes, on le voit, est exclue : alors que l’un et la dyade définissent, chez Platon, un principe formel informant une puissance indéterminée, le pair et l’impair constituent ici deux substances corporelles aussi immanentes l’une que l’autre (Aristote, Physique, III, v, 204 a 29).

La question fondamentale concerne, bien entendu, la conception du temps. Si l’éloquence des sources sur ce point est à la mesure du silence initiatique de Pythagore, le nombre limité des principes auxquels les pythagoriciens ramènent la variété du monde réduit quelque peu la marge de l’erreur. Les pythagoriciens réifient le temps. Ils accordent le statut de substance à une limite et à un illimité que la logique enseigne à ranger parmi les accidents (cf. la réaction d’Aristote, Physique, IV, vi, 214 b 22). A preuve, l’affirmation d’Aristote suivant laquelle « selon Pythagore, le temps est la sphère de l’enveloppe [du monde] » (Doxogr. Graeci, I, xxi, 1 ; cf. Présocratiques 58, B 33). L’idée du temps comme “mesure du mouvement” est exclue. Le pythagorisme confond mesure et mesuré : le temps se confond avec la « sphère elle-même » (Aristote, Physique, IV, x, 218 a 33 ; cf. Présocr. 58 B 33). A chaque corps son rythme, à chaque planète son nombre, à chaque processus évolutif un trope spécifique. Il est très probable que le problème de la durée devait se poser dans des termes analogues à celui du système harmonique. Les hauteurs supposent le temps : l’acuité du son produit par les planètes dans leur course est directement proportionnelle à leur vitesse. De plus l’acuité des notes, à cette époque, relève de la densité des particules d’air et ce temps est conçu en termes spatiaux. En effet Zénon n’est pas encore de ce monde et si le nombre a pu générer le temps et l’espace, c’est en vertu de la valeur spatiale de ses composantes. A preuve, le récit cosmogonique de la naissance de l’espace, parfaitement analogue à celle du temps. Les pythagoriciens affirment eux aussi, l’existence du vide :

Il pénètre à travers le ciel même à la façon d’un souffle, comme si le ciel aspirait justement le vide, et le vide opère une délimitation des substances qu’il définit, en tant qu’il constitue une sorte de moyen de séparer les êtres qui forment une succession et, ainsi, de les définir. De plus c’est dans les nombres que le vide existerait d’abord, puisque c’est lui qui [distingue] et définit [chacune des] entités numériques. (Aristote, Physique, IV, vi, 213 b 22 ; Présocr. 58 B 30).

On trouve une description parfaitement analogue de la genèse du temps dans le traité consacré par Aristote à la Philosophie de Pythagore : « le ciel est un et […] de l’illimité, pénètrent en lui le temps, le souffle, et le vide qui sans cesse délimite les lieux de chaque chose » (Aristote, Fragments, 201 ; Présocr. 58 B 30). L’équivalence établie entre le temps, l’air et l’illimité suppose la présence, dans la durée, de composantes élémentaires, analogues aux éléments du nombre. Simplicius nous informe que les pythagoriciens rapportaient au mouvement et au temps la cause de l’indétermination, « puisque l’indéterminé devient » (Simplicius, In Arist. Phys., 431, 13 ; Présocr. 59 B 30). Il est probable qu’on distinguait un temps “impair”, un temps “pair” et un temps “mixte” ou harmonisé.

A son état pur le temps “impair” comporte une négation du devenir. Si sa force centripète n’avait pas été entravée par le pair, le temps historique ne se serait jamais déployé dans l’espace. Illimité et inégal à lui même, son antagoniste “pair” habitait, avant la naissance de l’espace et du temps, les parties périphériques du ciel, en même temps que le souffle indéterminé. Aspiré par le monde au berceau, il divisa la première unité en deux, en trois puis en une multitude discrète d’instants impairs séparés dans leurs interstices par du temps indéterminé. C’est ainsi qu’il divise l’avant de l’après ; il gonfle et divise les instants, causant le devenir et le vieillissement des êtres. Il est vraisemblable qu’on ait tiré parti de ce genre d’arguments pour expliquer la compression des heures entre l’été et l’hiver. L’heure grecque, en effet, est une heure diurne, que l’on détermine en divisant en un même nombre de parties une quantité variable de lumière. La croyance dogmatique dans l’existence d’unités indécomposables devait conduire les pythagoriciens à décomposer le temps en instants discrets dotés d’une étendue élastique, ou, du moins, séparés par des interstices variables. Que l’aigu et le grave supposent une différence de densité au niveau des particules d’air qui composent le son est un lieu commun accrédité par la physiologia ionienne ; et la thèse d’une compression des instants ne paraît pas invraisemblable dans un contexte qui prête au temps et à la durée une valeur spatiale.

Enfin le pair et l’impair se mêlent, à l’instar de l’Autre et du Même dans le Timée de Platon, dans le contrepoint des révolutions astrales. Il peuvent générer des périodes commensurables ou incommensurables. Lorsque deux rotations s’accordent en vertu d’une mesure commune, le temps est une oscillation périodique définie par un décalage diamétral et un retour à un point de départ isochrone. La croyance dans le retour cyclique de l’histoire est alors une conséquence logique⁷ : la vertu modératrice de l’impair empêche l’évolution cyclique du temps de se visser, entraîné par des périodes irrationnelles, dans un devenir sans fin. Et c’est probablement à la lumière de ces considérations qu’il convient d’interpréter l’aphorisme d’Alcméon de Crotone suivant lequel « ce qui fait que les hommes meurent c’est qu’il ne leur est pas possible de joindre le commencement et la fin » (Aristote (Pseudo-) Problèmes, XVIII, iii, 916 a 33 ; Présocr. 24 B 2).

Le pythagorisme en somme qualifie l’instant. De même que l’arithmétique et l’harmonique définissent des quantités meilleures que d’autres, la réflexion du temps distingue des moments propices et inopportuns, définis par des relations qualitatives et des nombres. On trouve quelques éléments de cette optique dans les doctrines du temps critique (kairos) à laquelle les Pythagoriciens ont ménagé une place importante. Issu de la racine ker, le mot kairos établit une consonance avec le vocabulaire technique de la rupture. On y trouve les mots “crise”, “critique”, “discrétion”, “séparation”, “discrimination”, “jugement”, “décision”. Au sens large kairos désigne le moment critique où tout système en équilibre peut basculer dans un sens ou dans l’autre. Le mot apparaît dans l’épopée avec une forte connotation spatiale : il désigne un point vital, situé à l’endroit où la clavicule sépare la poitrine du cou, où le coup que l’on porte à l’adversaire peut se révéler décisif. Il est synonyme de symmetros.

L’idée de relation intervient lorsque le mot kairos désigne le point de convergence d’un système complexe de tensions antagonistes. Son symbole est alors la corde de l’arc qui agit sur la flèche, et le trait qui atteint la cible. Le rapprochement entre ce point de tension (tonos) et la tension des cordes sur la cithare se trouve chez Héraclite. Dans le corpus hippocratique, kairos désigne un point critique, particulièrement sensible, dans l’axe du temps (akmé, krisis) où la destinée du malade, en équilibre entre le bonheur ou l’infortune, subit un revirement (metabole) :

Ainsi tout témoigne que toute chose ayant même composition est assujettie à la condition naturelle de passer par des changements suivant des époques régulières. En chaque cas se manifestent quelques-unes des choses qui vont et qui viennent. Dans l’année accomplie surgissent beaucoup de maladies et s’opèrent beaucoup de guérisons suivant la proportion de temps en mois et en jours. Les jours les plus significatifs sont le premier et le septième, tant pour les maladies que pour le foetus ; c’est en effet durant ces jours que surviennent la plupart des avortements […]. Le même raisonnement s’applique aux jours critiques […]. En effet le médecin qui désire aller droit au salut des malades doit avoir l’œil sur tous les jours impairs, et, parmi les jours pairs, sur le quatorzième, le vingtième et le quarante-deuxième. En effet, cette limite (horos) est mise par quelques-uns à la théorie de l’harmonie, et c’est le nombre complet ; pour quelle raison, c’est ce qu’il serait trop long présentement d’expliquer. Il faut étudier ainsi les triades et les tétrades de jours : les triades en les joignant toutes (synemmenais hapasais) ; les tétrades en les joignant deux à deux et en les accouplant deux à deux (duo de para duo synemmenais) (Hippocrate, « Du foetus », 9, VII, 448).

L’interprétation de ce texte a posé quelques problèmes. C’est à Armand Delatte que revient le mérite d’avoir décrypté pour la première fois son sens exact (Delatte 1930). L’idée que les crises fébriles préfèrent certains jours plutôt que d’autres conduit les médecins à établir des systèmes de jours, qui sont à la durée ce que les systèmes harmoniques sont aux hauteurs. Les tétrades de jours s’articulent comme les tétracordes. Une tétrade vaut autant qu’une quarte ; une semaine autant qu’une septième. Comme dans les tétracordes, leur articulation peut donner lieu à un système conjoint (synemmenon) ou à un système disjoint (diezeugmenon). L’auteur des aphorismes décrit un système parfait classique, défini par deux tétracordes conjoints aux extrémités et un ton disjonctif séparant deux tétracordes disjoints au centre.

L’auteur des Aphorismes affirme que

le quatrième jour est indicateur du septième ; le huitième est le commencement d’une seconde semaine ; il faut considérer le onzième, car c’est le quatrième de la seconde semaine ; derechef il faut considérer le dix-septième car c’est d’une part le quatrième à partir du quatorzième, d’autre part le septième à partir du onzième (Hippocrate, « Aphorismes », IV, 477).

Le ton disjonctif divisant l’octave en une quarte et une quinte confère à cette série la valeur d’un système immuable (ametabolon). Sa suppression produit une succession de deux tétracordes conjoints. La présence de deux tétracordes de même poids introduit une ambiguïté fondamentale qui fracture le système en deux parties, par dichotomie. Parvenue à ce point la ligne mélodique bifurque (Aristoxène) dans une région inattendue de la voix, aiguë ou grave, faisant « perdre à l’esprit le fil du chant accoutumé et attendu ».

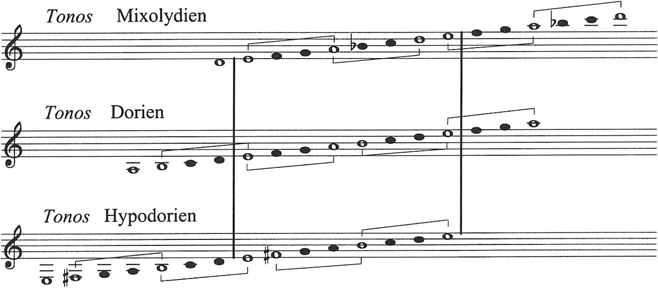
On trouve une application de cette mécanique dans un passage du Pronostic :

Le même nombre de jours qui amène la guérison ou la mort des malades règle les crises des fièvres. Les plus bénignes, celles qui portent, avec elles-mêmes, les signes les plus rassurants, se terminent en quatre jours ou plus tôt ; les plus malignes, celles qui sont accompagnées de signes les plus menaçants, tuent en quatre jours ou plus tôt ; telle est la limite de leur première période. La seconde période arrive au septième jour ; la troisième au onzième, la quatrième au quatorzième ; la cinquième au dix-septième ; la sixième au vingtième. Ainsi ces périodes des maladies les plus aiguës vont, de quatre en quatre jours, jusqu’au vingtième […]. Au delà, par un même calcul et par une même progression, on trouve une première période qui est de trente quatre jours ; puis une seconde qui est de quarante ; et une troisième qui est de soixante (Hippocrate, « Pronostic », IV, 477).

L’affirmation suivant laquelle le 17^ème jour est le 4ème après le 14^ème, prouve que la série progresse par continuité. Au lieu de recommencer le calcul des tétrades le 15^ème jour, l’auteur du « Foetus de sept mois » supprime la disjonction entre la nete hyperbolaion du hypate hypaton du premier système parfait. La mélodie dévie dans un système plus grave d’un ton. Comment interpréter les valeurs 34, 40, 60 ? Faut-il joindre une nouvelle tétrade au vingtième jour ? La méthode la plus sûre consiste à compter à rebours à partir de 34. On trouve alors deux tétrades conjointes entre 28-31 et 34 (sol). Les valeurs de 40 et 60 confirment celle de 20, terme de la sixième période, et la régularité du calcul exclut la possibilité d’une erreur de calcul dans le texte.

L’auteur du Pronostic attribue ce rythme « aux maladies plus aiguës ». L’ordre de succession de ses tétrades, en effet, contredit les lois de l’harmonie. Franchissant systématiquement le cadre de ses limites, sa forme parcourt le temps en hélicoïdale. Il s’agit d’une fièvre modulante, déviante, multiple, inégale à elle-même ; une fièvre “paire”, puisque c’est l’équipollence des tétracordes qui entraîne les systèmes dans leur déviance.

Toutes ces spéculations supposent, on l’a vu, une conception qualitative de l’instant. Ce qui paraît moins évident, en revanche, est de savoir si la détermination de cette qualité appartient à la relation établie par les unités, aux seules unités, ou bien aux deux. La scansion par tétracordes du paroxysme fébrile apporte une réponse affirmative à la première alternative. Le quatrième jour de la semaine, aux dires de l’auteur des Aphorismes, est « indicateur du septième » en vertu du rapport de consonance qui relie le milieu aux deux extrémités de la semaine : le quatrième jour opère une section arithmétique du septenaire (1 + 7/2) – et une division géométrique (12) de la septième (16 : 9). Cette attitude à l’égard du changement renvoie d’ailleurs à un modèle logique plus simple, universellement reconnu dans la physique présocratique et attesté, au début du V^e siècle dans le contexte de la médecine pythagoricienne, grâce à Alcméon de Crotone : la théorie de l’isonomie, de la crase ou, plus simplement, de l’harmonie. En effet la destinée du malade bascule en correspondance d’un point d’équilibre qualifié par un concours d’éléments antagonistes ; en l’occurrence, les éléments de la grammaire musicale : sons, intervalles et tétracordes. Les systèmes qui en résultent assument un caractère défini lorsque l’un de ses éléments parvient à établir son hégémonie sur son complément. Lorsque la mese divise l’octave en une quarte et une quinte, le système est parfait et immuable. Mais la succession de deux tétracordes conjoints génère un être inquiet à deux têtes, tiraillé en deux directions par l’équipollence de ses parties.

La relation, cependant, n’est pas le seul critère en matière de qualité. La détermination des qualités est d’abord du ressort des éléments du nombre : le pair déforme, l’impair maintient les choses telles qu’elles sont. Pair et impair imprègnent ensuite de leur substance les unités du système arithmétique ; et tout particulièrement la première, qualifiée de paire-impaire. Au grand scandale des pythagoriciens successeurs de Platon, les pythagoriciens présocratiques affirment à la fois l’indivisibilité de l’unité et son caractère composite. Aristote est formel : le noyau générateur du monde a commencé à se diviser par mitose parce qu’il enfermait en son sein la cause de sa propre transformation (le pair). Le pythagorisme, enfin, qualifie le nombre en soi et puis ses relations. A preuve, la présence, dans le système des disciplines cognitives, d’une arithmétique et d’une théorie harmonique, consacrées respectivement à la considération des nombres en soi, et à leurs relations mutuelles.

Ce temps-nombre ne s’inscrit pas nécessairement dans un système proportionnel et il ne crée pas nécessairement d’échéances périodiques. On en trouve des traces, au VII^e siècle, chez Hésiode :

Le douzième [jour du mois] est bien meilleur que le onzième : c’est celui où l’araignée volante file les fils de sa toile, à l’époque des longs jours, tandis que la Prévoyante [la fourmi] amasse sa récolte. C’est ce jour-là que la femme dresse son métier et entame son ouvrage. Mais méfiez-vous du treizième jour du début du mois pour vous mettre aux semailles (Hésiode, Les travaux, 775).

La qualité du temps des Travaux et les jours ne doit rien à l’idée d’une mesure du mouvement ; elle se confond avec l’objet qui la véhicule, elle obtient son caractère, de surcroît, par les objets qu’elle est censée dénombrer ; elle varie en fonction de la quantité élastique des jours. « Le grand vingtième, dans la saison des longs jours, que naisse un juge, et le voilà doué d’un esprit fort subtil » (Hésiode, Les travaux, 790). A chaque phénomène son temps ; à chaque processus évolutif un rythme biologique spécifique, difficile à intégrer dans une mesure unifiée. D’où l’idée d’un temps de la fatalité, qui scande l’imprévu, où le hasard règne en maître. Un fragment célèbre d’Héraclite compare ce temps à un enfant capricieux, jouant à la petteia avec la destinée des hommes. Dans la statuaire, le temps critique assume l’apparence d’un jeune homme au pieds ailés, en équilibre sur une sphère, tenant dans une main un rasoir supportant le fléau d’une balance. Fugitif, il est difficile à prévoir : il vient à notre rencontre en courant ; il faut l’arrêter par la longue chevelure qui tombe sur son front. Après son passage, impossible de le rattraper : il n’a pas de cheveux sur la partie postérieure de son crâne.

On dispose d’assez d’éléments pour formuler quelques hypothèses quant aux conséquences concrètes de ces doctrines pour l’histoire de la théorie musicale. La question essentielle dans toute cette discussion est de savoir si la qualité d’une structure mathématique fait corps avec les éléments qui la véhiculent ou bien si elle relève d’une forme abstraite informant une matière passive malléable, qui oscille dans ses qualités accidentelles tout en restant essentiellement la même. Or, les pythagoriciens ne séparent pas le nombre (Aristote, Métaphysique, 987 b 26ss ; 1080 b 16 ; 1090 a 22). L’idée d’une dichotomie forme-matière est exclue. La qualité, dans ces conditions n’est pas un attribut mais une propriété de la masse engagée dans la matière : la chaleur se confond avec le feu, la froideur avec l’eau, la sécheresse avec la terre. Immanence et discontinuité opèrent alors comme deux conditions réciproques. L’incapacité à concevoir le caractère d’une substance dans une catégorie abstraite, indépendante de ses composantes élémentaires, conduit la pensée à concevoir la tiédeur de l’eau sous la forme d’une mixtion de particules de feu et d’eau, et non comme un état d’un même élément. Il en va de même pour la durée et les hauteurs. Rythmos et rythmizomenon, hauteur et valeur (dynamis) des notes se confondent.

Et la qualité des rythmes et des modes est inséparable du “substrat” qui les véhicule. Le caractère est avant tout une propriété des éléments de la grammaire musicale et non une instance de leurs relations dans la mélodie. C’est une conception de ce genre qui a présidé à l’attribution de caractères spécifiques aux mesures, aux notes et aux modes. Le spondée est calme, le trochée agité ; l’harmonie dorienne est stable, la lydienne relâchée est orgiaque. La théorie musicale grecque prête d’ailleurs un caractère (ethos) spécifique à chaque note. Il s’agit d’un point d’importance capitale : dans ces conditions, l’altération des échelles suppose une mixtion de notes de qualité différente et non une modification dans leur forme ou ordre de succession. Dans la mesure où la théorie ignore la dichotomie entre la valeur des notes et leur hauteur, une modification formelle telle que la permutation cyclique des mêmes intervalles n’est d’aucun secours pour transformer le caractère d’un mode. On peut recombiner les parties sans obtenir aucun résultat. La seule attitude possible est une mutilation du mode, qui assume des caractères différents en vertu de la présence ou de l’absence de certaines notes à la qualité préétablie. On trouve des traces de cette attitude à l’égard du changement dans les renvois du traité attribué à Plutarque aux règlements en vigueur dans le concours musicaux interdisant le recours à certaines notes dans un certain genre de mélodie.

Un témoignage conservé par Aristide Quintilien place le musicien Damon d’Athènes, éducateur satellite de Périclès, dans une posture analogue à celle d’un pharmacien occupé par la confection d’un médicament. Avant d’administrer un régime de gammes adapté à chacun de ses patients, il façonne ses échelles sur mesure, en essayant d’imiter par des sons la mixtion du tempérament individuel. Il distingue des sons masculins, féminins et mixtes, qu’il fait entrer dans ses échelles selon un dosage variable. Afin de moduler leur caractère, il procède en anatomiste à l’ablation de leurs qualités, supprimant quelques-unes d’entre elles ou en diminuant leur présence statistique.

En effet les notes d’une mélodie continue façonnent, par assimilation, le tempérament des enfants et des gens plus âgés […] c’est aussi ce que Damon s’efforçait de mettre en lumière. Et d’ailleurs dans les gammes qu’il a transmises à la postérité, il est possible de découvrir que tantôt ce sont les notes féminines qui prédominent, tantôt les notes mâles qui prédominent ou se font rares jusqu’à disparaître totalement ; cela montre avec évidence que le tempérament de chaque âme réclame une harmonie particulière (Présocr. p. 459).

Cette attitude à l’égard du changement n’est pas spécifique à la seule théorie musicale. Dans l’une de ses odes, Pindare s’est amusé à priver l’alphabet de l’un se ses éléments. Et la légende veut que lorsqu’on demanda à Pythagore d’apaiser la colère d’un jeune homme enivré par un rythme effréné à 5/8, il ordonna de changer radicalement de pied et non de procéder, conformément aux principes énoncés par Aristoxène, à une division différente du même vers.

Une phrase célèbre, prononcée en 1951 par le musicologue hongrois Otto Gombosi, voudrait que la musique de l’Antiquité grecque ait toujours ignoré les modes ; thèse que récemment Johannes Lohmann a essayé de maintenir en vie, affirmant que « la réalité proprement dite dans la musique grecque est le système des tonoi, et cela dès le début » (Lohmann, p. 72). Quant à la métrique, la thèse suivant laquelle la théorie d’Aristoxène peut contribuer à la compréhension de la métrique du vers grec jouit encore d’un certain crédit. Or, les vicissitudes subies au cours des siècles par le concept d’harmonie comme l’histoire des idées en matière de changement qualitatif apportent un démenti à ces assertions. La théorie des tonoi avec son corrélatif rythmique serait inconcevable en dehors du contexte aristotélicien dont sont issues la dichotomie forme-matière, l’idée d’une puissance (dynamis) des notes et la doctrine de l’altération.