Il existe une consonance, une relation – non de cause à effet, mais plutôt un parallélisme – entre l’expérience musicale et certains problèmes de la science d’aujourd’hui tels que les bifurcations, les phénomènes de cohérence et les corrélations. Le temps et la durée y apparaissent comme des notions fondamentales. Tant en musique qu’en physique, la composante temporelle joue un rôle essentiel : il n’y a pas de forme musicale sans le déroulement du temps. Il s’inscrit dans la musique une irréversibilité fondamentale : son expression n’a d’existence matérielle ni en deçà ni au-delà du temps pendant lequel elle se déroule. Avec cette particularité que la forme sonore n’est sous-tendue que par la seule dimension du temps. C’est ce qui, en regard de l’infinie complexité des multiples formes artistiques, rend la musique plus accessible à l’analyse quantitative. En particulier une séquence musicale peut être considérée comme un phénomène physique régi par l’évolution au cours du temps d’un signal acoustique. Selon cette interprétation, la séquence musicale se traduit dans le langage de la physique comme une série temporelle. Elle devient dès lors susceptible d’être analysée avec les outils que la physique et les mathématiques modernes ont construits pour décoder la dynamique de phénomènes complexes tels que le chaos et la turbulence. Les concepts de dimensionnalité et d’entropie – notions essentielles en théorie des systèmes dynamiques – doivent être redéfinis pour être appliqués à l’analyse de la dynamique temporelle en musique. Ces grandeurs peuvent alors être explicitées et quantifiées ; l’analyse qui en découle est appliquée à des pièces échantillonnées dans la littérature musicale du XVII^e au XX^e siècle.

Il n’y a pas de continuité dans l’univers musical : la musique naît du silence et retourne au silence.

Dans cette alternance de création et de disparition, le temps joue un rôle essentiel et particulier auquel la description mécaniste qui nous vient essentiellement de la physique, et plus précisément des phénomènes périodiques, ne s’applique pas. Dans l’expérience musicale une structure temporelle se développe qui brise le rythme régulier, et crée une libération par rapport au temps de l’horloge. On pourrait ainsi parler d’une durée bergsonienne en musique : il y a éclatement de la notion d’instant. En physique, l’instant est un point défini entre un intervalle qui précède et un intervalle qui suit. En musique, la notion de présent change de signification : il se produit une délocalisation du temps que l’on vit, un effacement des limites entre le monde intérieur et le monde extérieur. Lorsque le musicien déchiffre ou interprète, il suit un objet qui est donné mais qui devient partie de lui-même au moment où il joue. La différence entre extérieur et intérieur s’efface. Cet effacement devient particulièrement significatif dans la musique de chambre ou la musique de jazz : le musicien qui participe à l’action de ses partenaires est, en terme de langage de la physique, délocalisé. Ainsi la musique rejoint le problème ontologique, c’est-à-dire le problème fondamental de la distance entre l’individu et le milieu dans lequel il se trouve.

La musique prise comme une donnée, s’apparente à un code biologique. Bien qu’elle puisse être analysée en fragments, une pièce de musique forme un tout : chaque partie doit être perçue par rapport à l’entièreté de l’œuvre. Il n’y a pas de fragmentation possible, comme il ne peut y avoir fragmentation d’une molécule biologique si celle-ci doit assurer sa fonction organique.

L’histoire de la musique pose la question de la signification d’un art dont la conception a évolué. On a vu dans la musique une illustration de ce que l’on considérait à l’époque du quadrivium comme un élément fondamental de la connaissance. Ainsi, la conception pythagoricienne s’organise autour du fait qu’aux sons correspondent des nombres et à l’harmonie des rapports simples. La conception pythagoricienne a joué un rôle crucial dans l’histoire de la pensée humaine ; on y a trouvé la preuve qu’au moins une part de notre expérience sensible est écrite en termes formels. Cette constatation a fortement impressionné les savants qui ont formulé la science occidentale au XVII^e siècle. En particulier Kepler, mais aussi Descartes et Galilée, ont toujours insisté sur le fait que la nature devait être décrite en nombres. Il y a bien sûr diverses descriptions possibles de la nature autres que la formalisation mathématique ; néanmoins, que ces penseurs affirment avec une quasi certitude, presque une ferveur religieuse, que la nature est écrite en nombres apparaît vraisemblablement comme un souvenir du pythagorisme.

Au XIX^e siècle, la musique devient aussi objet de métaphysique et d’esthétique. Schopenhauer y voit une réalité fondamentale, une expression des lois de l’univers ; pour lui, métaphysicien, ces lois sont une forme d’expression, une volonté, proches de l’élan dont parle Bergson. La musique nous transmet une vérité : elle nous parle de caractéristiques fondamentales de l’univers. Pour formuler les lois de la musique et comprendre ce qu’elle est, il faut faire appel à des notions importantes parmi celles qui vont constituer la base de la physique de la seconde moitié du XX^e siècle. C’est somme toute inattendu que la musique ne soit plus aujourd’hui un phénomène marginal – un jeu partiellement lié au hasard – mais l’expression dans le domaine culturel d’un reflet des lois fondamentales. D’autre part la musique est apparue comme une activité biologique bien avant qu’on établisse le code génétique. Darwin voyait dans la musique un élément de l’évolution biologique lié à la possession et à la défense du territoire, participant au processus de sélection. Pour juger aujourd’hui de la musique comme jeu, comme problème biologique ou comme réalité fondamentale, on doit nécessairement comparer le phénomène musical (ou le texte qui lui sert de support) à l’image que l’on se fait du monde. La musique est un art du temps, qui implique une organisation temporelle. Les physiciens et les mathématiciens analysent ce type d’organisation dans les phénomènes naturels en utilisant la notion de série temporelle.

Les séries temporelles se répartissent entre deux cas extrêmes : les séries périodiques et les séries aléatoires (par exemple la série périodique à deux valeurs : 010101010101., et la série aléatoire : 011100110110001…). Nous verrons comment caractériser les séries temporelles musicales qui ne sont des séries ni purement aléatoires ni simplement périodiques. Le signal acoustique le plus simple est un signal périodique correspondant à une seule fréquence. D’autre part un signal très complexe est le bruit blanc : toutes les fréquences y sont présentes et il en résulte l’absence totale d’organisation temporelle. Parallèlement à l’analyse en terme de fréquences, on utilise volontiers une description exprimée à l’aide de la variable temps. La fréquence étant l’inverse d’un temps, les deux représentations sont en principe équivalentes. Toutefois, la description temporelle s’avère plus représentative lorsqu’on considère la fonction d’auto-corrélation qui contient la “mémoire” du phénomène : combien de temps le souvenir d’un son persiste-t-il ? C’est la mesure de la persistance du phénomène à laquelle la fonction d’auto-corrélation nous permet d’accéder. Dans le cas d’un signal périodique, la mémoire persiste uniformément – il y a corrélation forte d’un instant à l’autre – tandis que dans le cas du bruit blanc pour lequel les signaux ont lieu au hasard – la corrélation est strictement nulle – il n’y a aucune mémoire. Où se situe le “signal” musical selon ce type de critère ?

Nous pouvons donc penser de façon équivalente soit en temps, soit en fréquence, et le passage de l’un à l’autre se fait par la transformation de Fourier. En termes de représentation en fréquence, ce que l’on qualifie de musique n’est certainement pas le bruit blanc qui ne donne aucune impression de contenu musical, ni le phénomène périodique qui engendre la monotonie. Le phénomène musical possède une certaine cohérence, intermédiaire entre l’aléatoire et le périodique : il y a des corrélations, mais pas de structure strictement déterministe. Une partie d’un morceau de musique présente des corrélations avec celles qui suivent, mais connaissant uniquement une partie on ne peut prédire tout ce qui se produira ultérieurement, comme on peut le faire pour un phénomène périodique.

La musique possède une symétrie brisée : elle se déroule selon un ordre temporel. Comme un texte, la musique se lit suivant une direction qui exclut la symétrie temporelle de la lecture. La notion de temps galiléen, dans lequel tous les instants sont équivalents, est brisée : les instants ne sont pas invariants par rapport au début et à la fin de l’œuvre.

Ainsi apparaissent certaines caractéristiques générales : corrélations, absence de déterminisme, symétrie brisée. La musique étant produite par l’homme peut être considérée comme un phénomène naturel. Et c’est précisément une des questions que se pose le physicien : comment des objets à symétrie brisée et présentant des corrélations apparaissent-ils dans la nature ? Dans la mesure où l’on peut répondre à cette question, quelle serait, par rapport à ces objets naturels, la situation particulière de la musique ?

L’existence d’objets à symétrie brisée et à corrélations n’est pas “naturelle” dans le cadre de la physique classique qui est une physique du déterminisme et de la réversibilité. Les objets qui nous préoccupent y sont étrangers ; ceux de la physique classique sont des phénomènes périodiques modèles comme les mouvements de la terre autour du soleil ou de la lune autour de la terre, où le temps n’a pas de direction privilégiée. Ce sont des phénomènes réversibles : le mouvement peut se faire indifféremment dans l’une ou l’autre direction. Du point de vue de la physique classique, les phénomènes musicaux sont, en quelque sorte, des intrus. En revanche dans la physique telle qu’elle se construit aujourd’hui, ils trouvent une place naturelle parmi les phénomènes irréversibles.

Alors que la physique classique est avant tout basée sur des modèles mécaniques, périodiques et réversibles, dès le début du XIX^e siècle, une seconde physique, émanation d’un monde industriel naissant, vient se placer en contrepoint : c’est la physique des transformations, des processus irréversibles, des phénomènes non-linéaires, des transitions loin de l’équilibre. Un principe fondamental est formulé en 1865 : c’est le célèbre second principe de la thermodynamique, selon lequel l’entropie d’un système croît jusqu’à ce que celui-ci ait atteint son équilibre. Alors que le monde de la physique classique est figé et immuable, le monde thermodynamique a une histoire, une histoire de dégradation où l’entropie croît jusqu’à ce que tous les phénomènes irréversibles possibles y aient eu lieu. A ce moment tout s’arrête : le système a atteint son état d’équilibre. Pendant le XIX^e siècle et jusqu’au début du XX^e siècle, c’est cet état final qui fait l’objet principal des préoccupations scientifiques. Ce n’est qu’au cours des dernières décennies qu’on s’intéresse aux mécanismes, non pas de la disparition des structures (au cours de l’évolution vers l’équilibre) mais au contraire de la création des structures. Comment des structures naissent-elles ? Une théorie qui peut expliquer leur disparition – l’approche vers l’uniformité – doit aussi pouvoir expliquer leur apparition. Loin de l’équilibre, lorsqu’un système est maintenu sous contrainte (de telle sorte qu’il ne puisse évoluer vers l’équilibre), des structures peuvent naître et des situations nouvelles peuvent apparaître qui étaient inconnues de la physique classique.

Qu’est-ce qu’un système maintenu loin de l’équilibre ? C’est, par exemple, un réacteur chimique qu’on entretient afin que les réactions qui s’y produisent ne s’arrêtent pas. C’est aussi une ville qui ne vit que parce qu’il s’y produit des échanges avec ce qui l’entoure. Ce sont des systèmes en forte interaction avec l’environnement. On va donc s’intéresser à des systèmes ouverts dans lesquels la relation avec le monde qui les entoure les empêche de s’éteindre. Pourquoi dans ces systèmes (loin de l’équilibre) des structures nouvelles ignorées de la physique classique deviennent-elles possibles ? Considérons que nous mesurions la distance à l’équilibre à l’aide d’un paramètre. Ce paramètre est une mesure de l’amplitude de la contrainte exercée sur le système. Lorsque le système est près de l’équilibre, la valeur de ce paramètre est petite ; on peut alors écrire des équations linéaires en ce paramètre et les systèmes linéaires ont en général une et une seule solution. Loin de l’équilibre, il n’y a plus de petit paramètre et le système n’est plus décrit par des équations linéaires. Les effets ne sont plus simplement proportionnels aux causes ; ils sont liés à des puissances élevées de ces dernières et varient fortement et vite lorsque la cause change peu. Les équations non-linéaires admettent de multiples solutions en fonction de la gamme de valeurs que prend le paramètre.

C’est ainsi que dans ces systèmes non-linéaires apparaissent de nouveaux états physiques, organisés, cohérents, souvent complexes, résultant d’échanges où le monde extérieur apporte une énergie qui est transformée en structure. On cite volontiers l’exemple d’un liquide chauffé par dessous : il s’y forme des cellules de convections régulières. Comment une telle structure peut-elle apparaître dans un fluide où les molécules qui le constituent sont animées de mouvements au hasard ? Sous la contrainte thermique imposée par un gradient de température les molécules se mettent à se suivre les unes les autres sur des temps et des distances macroscopiques, formant ces cellules de convection dont chacune est constituée de milliards de molécules en mouvements cohérents. Il s’est donc créé un état cohérent avec des corrélations à longue portée. Une structure s’est formée brisant la symétrie d’espace. Il en est de même en musique où une symétrie brisée dans le temps l’est aussi dans l’espace de la partition.

Selon l’analyse mathématique, chaque fois que des structures apparaissent, que des formes se créent, c’est que les équations qui décrivent le système donnent naissance à des solutions nouvelles. Les points particuliers où ces solutions surgissent sont les points de bifurcation. A ce moment, l’ancienne solution devient instable et une nouvelle solution s’installe : une nouveauté radicale naît, des symétries se brisent et un changement d’espace peut avoir lieu. L’espace euclidien où tous les points et tous les instants sont équivalents, peut faire place à de nouveaux espaces et à de nouveaux temps. L’idée qu’à la bifurcation un nouveau phénomène émerge n’a pas d’équivalent en physique classique dont le prototype est le phénomène périodique où l’harmonie se perpétue indéfiniment. En physique non-linéaire la continuité harmonique est rompue et à chaque discontinuité correspond l’apparition de phénomènes qualitativement nouveaux.

Il est un autre aspect important des phénomènes que présentent les systèmes thermodynamiques : ils sont stables ou du moins possèdent un certain type de stabilité que n’ont pas les phénomènes de la dynamique classique. Imaginons qu’une comète passe au voisinage de la terre. La trajectoire de la terre sera légèrement déplacée et le restera après le passage de la comète. Il n’y a aucune raison pour que la terre revienne sur son ancienne orbite. La dynamique classique ne peut oublier les perturbations et est dans ce sens instable. Au contraire, dans les phénomènes dissipatifs, il y a perte de la mémoire des perturbations. Un pendule soumis au frottement finit par s’immobiliser. Si nous le perturbons en lui imprimant une nouvelle oscillation, il revient néanmoins vers le même point d’immobilisation. Ce point est un attracteur – plus précisément un attracteur ponctuel. Le pendule y retourne infailliblement : c’est un point fixe stable. Si les points attracteurs sont connus de longue date, ce qui est nouveau est qu’il existe des attracteurs plus compliqués : l’attracteur peut constituer une courbe. L’existence d’une courbe d’attraction est la signature d’un phénomène périodique privilégié vers lequel le système revient après avoir été perturbé. Il y a donc un phénomène de stabilité forte. Par exemple, les rythmes attractifs sont très importants dans les processus biologiques parce qu’ils assurent la stabilité et permettent la régulation. Mais il existe des attracteurs qui combinent à la fois stabilité et instabilité : ils sont stables dans une direction et instables dans une autre. Ce sont les attracteurs étranges.

Ces attracteurs traduisent des comportements beaucoup plus complexes. Il n’y a pas de stabilité dans le détail de la dynamique, mais sur une plage étendue finie de l’espace que le système explore. Il ne s’agit plus de phénomènes simplement périodiques, mais d’une combinaison subtile de comportements liés à la fois à des propriétés périodiques de stabilité et à des propriétés erratiques semblables à celles qui caractérisent le hasard. C’est le domaine du chaos (on parle de chaos déterministe lorsque les équations qui régissent ces phénomènes sont déterministes). C’est la raison pour laquelle ces attracteurs étranges sont aussi appelés attracteurs chaotiques.

Revenons à la série temporelle. Celle-ci constitue en quelque sorte la représentation de la dynamique du phénomène. Codons cette série à l’aide de caractères alphabétiques. Dans le cas d’un phénomène périodique sa représentation serait par exemple une chaîne telle que XYZXYZXYZ… Si le phénomène est chaotique le texte que nous obtenons serait plutôt XZYXYZYZZYXZXYXZ… qui n’est ni répétitif de façon régulière, ni désordonné de manière aléatoire : en quelque sorte un intermédiaire à mi-chemin entre le signal périodique et le bruit blanc. En termes de langage des probabilités, c’est une chaîne à caractère stochastique, en ce sens que connaissant un morceau du texte, nous pouvons faire quelques prédictions sur ce qui va suivre, mais ces prédictions perdent toute pertinence lorsque nous progressons plus avant. C’est ainsi que nous avions caractérisé très schématiquement la musique. Étant donné par exemple une tonalité nous pouvons estimer quelle est la probabilité de telle ou telle modulation, mais nous ne pouvons pas faire de prédiction sur la pièce entière. Aucune partie prise séparément ne permet d’appréhender la structure de l’ensemble.

L’information contenue dans une chaîne de caractères est proportionnelle à la longueur du texte. En outre, le texte obtenu par codage de la série temporelle d’un phénomène à symétrie brisée a une direction de lecture ; la chaîne présente les bonnes corrélations quand elle est lue dans le sens imposé par la brisure de symétrie. Longueur de chaîne et direction de lecture sont donc des facteurs essentiels du contenu d’information.

Dans la nature nous sommes entourés de phénomènes qui sont décrits par des attracteurs chaotiques. Pour certains phénomènes dont on a reconstitué la série temporelle à partir des variations d’une grandeur caractéristique mesurée au cours du temps, le tracé est irrégulier sans qu’il ne s’agisse pour autant de fluctuations typiques d’un bruit blanc. Pour déceler la dynamique des phénomènes, on peut calculer la fonction d’auto-corrélation de la grandeur et évaluer ainsi les corrélations qui existent entre une valeur et celles mesurées à des instants ultérieurs. Ceci mettra éventuellement en évidence un “effet de mémoire” dans le processus dynamique et le cas échéant permettra d’estimer la durée de cette mémoire. Une autre manière de procéder consiste à construire un espace abstrait, l’espace des phases, dans lequel on représente selon trois axes, les valeurs décalées dans le temps de la grandeur mesurée. A chaque point de cet espace correspondent trois valeurs décalées par rapport à un temps donné, et à chaque instant correspond un point. En procédant de la sorte on obtient une trajectoire dans l’espace des phases qui constitue la représentation spatiale de l’évolution temporelle du phénomène. En analysant ce portrait de phase – la forme de la trajectoire et sa densité – on peut se faire une idée du système dynamique sous-jacent. En général, la grandeur accessible à la mesure (ou les quelques grandeurs accessibles en nombre très restreint) dépend (ent) d’un grand nombre de variables qu’il est impossible de maîtriser. Toutefois le nombre de variables nécessaire et suffisant pour déterminer la nature de la dynamique est nettement inférieur au nombre total de variables qui interviennent dans l’ensemble des processus qui gèrent le système. C’est précisément là que réside l’élégance de l’analyse des portraits de phase. La dimension minimale de l’espace des phases susceptible de contenir la trajectoire correspond au nombre nécessaire et suffisant de variables. Et la trajectoire immergée dans cet espace constitue un objet de dimension nécessairement inférieure (ou égale) à celle de l’espace. L’analyse basée sur ce type de représentation en terme du portrait de phase montre que pour les systèmes à dynamique complexe, la trajectoire dans l’espace des phases forme un de ces attracteurs étranges qui sont la signature d’une dynamique régie à la fois par des oscillations et par des changements très violents. Ce sont des phénomènes hautement instables, mais qui peuvent se décrire fondamentalement par un petit nombre de variables.

Cette nouvelle vision change profondément le sens de notre dialogue avec la nature. La perception de l’importance des systèmes dynamiques à petit nombre de variables montre que la complexité qui nous entoure ne peut être éludée par une analyse détaillée de causes multiples, voire innombrables. Il s’agit d’une complexité intrinsèque qui écarte à jamais cette harmonie simple et régulière dont rêvait la physique classique. Il existe une complexité à caractère aléatoire irréductible au delà de laquelle toute simplification est exclue. Connaissant, par l’expérience ou par le calcul, une série temporelle, nous possédons aujourd’hui des méthodes pour déterminer quel type de système dynamique, quel type de mécanisme a pu engendrer cette série. C’est un résultat d’importance dans l’histoire de la science actuelle. Parce que cette approche va plus loin que les analyses qu’on pratique habituellement. Transformer une série temporelle en série de Fourier revient à remplacer une variable temps par une variable fréquence, mais ne permet pas pour autant de comprendre la dynamique sous-jacente. Or, il s’agit de cerner la complexité du système qui a donné naissance à la série temporelle. La même question se pose à propos de la musique : quel est le mécanisme qui donne naissance à la série temporelle musicale ?

D’aucuns, tel Leibniz, considèrent la musique comme l’art abstrait par excellence et l’assimilent à une pure construction de l’esprit qui reposerait sur des principes sans équivalent dans la nature. Or, il y a une vingtaine d’années, deux physiciens de l’Université de Berkeley ont observé que l’évolution à long terme de séquences musicales, qu’il s’agisse de concerti de Bach, de symphonies de Beethoven ou d’enregistrements des Beatles, obéit à la même loi statistique que de nombreux phénomènes naturels, par exemple les variations de fréquence des crues du Nil ou les influx nerveux : l’énergie du son se répartit proportionnellement à l’inverse de la fréquence (1/f). Cette observation nous a intrigué et nous lui avons trouvé une explication théorique. Cette caractérisation en 1/f est intéressante parce qu’elle montre que la musique est soumise à des règles précises qui s’énoncent dans le langage de la physique contemporaine. Mais si toutes les formes musicales sont semblables par leur comportement dynamique à temps long, comment les distinguer les une des autres ? Car ces musiques se ressemblent aussi “vues de près”, à l’échelle de la dizaine de sons consécutifs, où les notes, les accords, les sons se succèdent suivant un schéma déterminé, donc facile à prédire.

En fait, c’est la dynamique à moyen terme qui marque la “griffe” d’un compositeur, voire d’une œuvre ou d’un style. Cette dynamique spécifique est toutefois beaucoup moins aisément accessible, car elle met en jeu toute la complexité de l’écriture musicale et le nombre de variables pertinentes défie toute velléité d’analyse quantitative. Les physiciens et les mathématiciens qui étudient les phénomènes dont l’évolution au cours du temps est complexe, par exemple un écoulement turbulent, ne savaient pas non plus au départ comment caractériser des situations aussi inextricables. La théorie des systèmes dynamiques a bousculé cet obstacle en permettant de représenter l’évolution du système sous forme de trajectoire dans cet espace abstrait, l’espace des phases. Les propriétés topologiques de ces trajectoires donnent la clé de la dynamique du système. En appliquant la même démarche, nous pouvons “matérialiser” les pièces de musique sous la forme d’objets spatiaux à partir de leur trajectoire dans l’espace des phases.

Voyons par exemple comment se construit cette trajectoire dans le cas d’un canon à trois gammes. Chaque voix déroule une gamme majeure alternativement ascendante et descendante sur trois octaves. Les corrélations entre notes successives d’une voix sont évidentes, mais tout se complique lorsqu’entrent la deuxième voix puis la troisième. Il devient alors impossible de démêler intuitivement l’écheveau des corrélations entre chaque note et l’ensemble des autres au cours du temps. Ici, l’espace des phases possède trois dimensions, une pour chaque voix, de sorte qu’un point de l’espace est caractérisé par les hauteurs des trois voix à un instant donné. La trajectoire du canon est donc la courbe que décrit ce point, autrement dit la séquence musicale, au cours du temps. Comme cette pièce est cyclique, la trajectoire est une boucle (voir Illustration IV). Mais ce n’est qu’un cas d’école. Dès que l’écriture et le discours musical s’enrichissent, le portrait de phase devient plus complexe.

La théorie des systèmes dynamiques étudie les phénomènes dont il est impossible de prédire exactement le comportement au cours du temps, bien que celui-ci soit régi par des équations connues. Les solutions de ces équations sont les trajectoires des particules ou des objets qui entrent en jeu dans le phénomène considéré. La difficulté vient de l’extrême sensibilité de leur comportement aux conditions initiales. Lorsqu’un système physique est soumis à une contrainte extérieure, il réagit proportionnellement à cette contrainte tant que la valeur de celle-ci est faible : c’est le domaine linéaire. Au-delà d’un certain seuil, l’effet engendré par la sollicitation peut dépasser largement l’amplitude de la contrainte ; lorsqu’il n’y a plus proportionnalité directe entre cause et effet, on pénètre dans le domaine non-linéaire. La plus infime imprécision sur les conditions initiales est susceptible de s’amplifier à tel point qu’il devient très rapidement impossible de prédire l’état ultérieur du système. C’est ainsi que deux feuilles mortes qui tombent dans un torrent côte-à-côte – les conditions initiales sont donc pratiquement identiques pour chaque feuille – vont suivre des trajectoires très rapidement divergentes, qu’il sera impossible de prévoir. Et pourtant, l’écoulement du torrent est régi par les équations différentielles de la mécanique des fluides, équations qui ont bien une solution exacte. Bien que le système soit déterministe, la présence de termes non-linéaires exclut leur résolution analytique explicite. La théorie des systèmes dynamiques contourne cette difficulté intrinsèque en donnant des informations à la fois qualitatives et quantitatives sur l’évolution du système au travers de son portrait de phase.

L’état du système dynamique que constitue une séquence musicale est caractérisé à chaque instant par diverses grandeurs, telle la hauteur du son de chaque instrument. Dans les pièces monodiques comme une suite pour violoncelle de Bach, un caprice de Paganini ou Syrinx de Debussy, une seule variable suffit. En général il en existe plusieurs qui dépendent les unes des autres et l’évolution du système est représentée par une trajectoire dans l’espace des phases dont la dimension est égale au nombre de ces variables. Cette trajectoire est le lieu de tous les points dont les coordonnées sont les valeurs prises par les variables au cours du temps.

Les portraits de phase des œuvres musicales constituent des trajectoires chaotiques avec une structure extrêmement ramifiée et irrégulière qui ressemble à celle des attracteurs étranges. Nous avons un moyen de les caractériser par leur dimension fractale qui mesure leur capacité à occuper l’espace dans lequel ils sont immergés.

En plus de la caractérisation topologique de l’attracteur, il existe une grandeur, l’entropie d’information, qui mesure le contenu d’information lié à l’évolution du système. Un pendule entretenu a une dynamique définie et prévisible, et toute mesure n’apporte aucune information nouvelle à la connaissance que nous en avons à partir d’une mesure initiale : l’entropie d’information du pendule est minimale et nous pouvons lui attribuer une valeur nulle. A l’opposé, chaque fois que nous effectuons une mesure sur un phénomène aléatoire, le résultat est nouveau en ce sens que notre connaissance d’un état antérieur du système ne nous permet en aucune manière de prédire l’état ultérieur. L’information est ici sans cesse renouvelée : l’entropie prend dans ce cas une valeur maximale (infinie pour un phénomène strictement aléatoire au sens mathématique). Pour un phénomène à dynamique complexe tel que le chaos déterministe, l’entropie d’information prend une valeur finie non-nulle.

Les concepts d’attracteurs, de dimensionnalité, d’entropie ont été intensivement utilisés dans l’étude de systèmes dynamiques qu’il s’agisse de modèles théoriques ou d’observations expérimentales en laboratoire ou dans la nature. Partant de l’idée que nous percevons la musique comme l’évolution au cours du temps de signaux acoustiques, nous pouvons associer au déroulement d’une séquence musicale la notion de série temporelle. D’où la question : comment identifier et caractériser la dynamique musicale à partir des principes de la théorie des systèmes dynamiques ?

L’idée peut se concrétiser de façon simple pour une pièce monodique comme une suite pour violoncelle de J.-S. Bach. La série temporelle est alors définie comme les variations de hauteur au cours du temps. D’autre part si nous songeons à toute la richesse harmonique et contrapuntique d’une suite de Bach, il est clair que la série temporelle que nous venons de définir ne met en évidence qu’une des variables du phénomène musical. Mais les variations temporelles de celle-ci résultent de toute la dynamique sous-jacente. Comment alors faire émerger cette dynamique à partir de l’analyse de la série temporelle ?

Nous procédons de la manière suivante. La pièce étudiée est jouée sur un clavier musical qui est interfacé à l’ordinateur ; un code transforme les impulsions mécaniques des touches du clavier en une série de données numériques qui sont alors mises en mémoire. Ces données correspondent à la hauteur et à la durée des notes jouées au clavier ; la séquence musicale est ainsi enregistrée sous la forme d’une série temporelle. L’ordinateur est programmé pour traiter cette série de manière à obtenir sa fonction de corrélation, et son spectre, ainsi que son portrait de phase. S’il s’agit d’une pièce à une seule voix, le portrait est réalisé par la méthode du décalage temporel. Pour les pièces à plusieurs voix (fugue, trio, quatuor,…), les voix sont enregistrées individuellement et synchronisées ensuite pour construire le portrait dans l’espace des phases qui a les dimensions d’un hypercube (tridimensionnel pour les pièces à trois voix, quadridimensionnel pour celles à quatre voix,…).

Comme nous l’avons vu, une gamme ascendante et descendante est un signal périodique ; son portrait de phases a l’allure d’un cycle (voir Illustration IV) de dimension un (celle d’un attracteur monopériodique). A l’opposé d’une séquence exempte de tout élément de surprise, considérons le cas de la musique aléatoire. Sur la base d’une génération de déplacements au hasard sur une étendue de quelques octaves, l’ordinateur est programmé pour “composer” une séquence musicale où la succession des intervalles de hauteur et de durée sont répartis de manière aléatoire sur chaque voix. Le résultat est une partition de “musique blanche” : son portrait de phase remplit tout l’espace du cube et est donc un objet de dimension trois (voir Illustration IV).

En appliquant la même procédure aux trois voix du Ricercare de l’Offrande Musicale de Bach, nous obtenons un objet immergé dans l’espace tridimensionnel du cube mais qui ne le remplit que partiellement (voir Illustration IV) : il a une dimensionnalité légèrement inférieure à deux. Le portrait de phase constitue donc une représentation spatiale dans cet espace abstrait qu’est l’espace des phases, de la dynamique temporelle de la séquence musicale, et sa dimensionnalité donne une mesure de la dynamique globale de la pièce.

Pour tenter de cerner la dynamique locale, nous faisons appel à la théorie de l’information. Une séquence de notes peut être considérée comme une chaîne de caractères. Lorsqu’elle est codée comme telle, elle peut être analysée du point de vue de son contenu d’information. La grandeur qui quantifie ce contenu, l’entropie d’information, mesure en quelque sorte le degré d’inattendu dans une succession d’événements. Dans une gamme, la séquence des notes est régie par une règle simple qui permet de prédire à partir d’une note, la valeur de la suivante. Donc ici, pas ou peu d’inattendu : l’entropie doit être voisine de zéro. En revanche, dans une musique aléatoire, rien de ce qui précède ne permet de préjuger de ce qui va suivre : l’entropie y est maximale. En pratique, l’entropie est une fonction de la probabilité d’occurrence d’un caractère – d’une note – parmi l’ensemble des caractères possibles d’un alphabet défini – des degrés possibles de la gamme chromatique. Une mesure plus fine consiste à mesurer cette probabilité compte tenu du ou des caractères précédents. Cette notion prend toute son importance dans le cadre de la musique tonale occidentale. Quelle est la probabilité d’apparition d’une note étant donnée la précédente, l’une et l’autre appartenant ou non aux degrés d’une tonalité de référence ? Ceci nous conduit à définir une nouvelle entropie, l’entropie paramétrée, par laquelle on quantifie la “diversité” des notes dans une séquence en terme de leur appartenance ou non à une tonalité de base. L’idée sous-jacente est de prendre en compte la liberté, les audaces du compositeur par rapport à la tonalité. Les écarts à celle-ci apparaissant comme des “événements inattendus” contribuent davantage à l’accroissement de l’entropie d’information. La notion d’entropie paramétrée est évidemment sans objet pour la gamme. D’autre part sa valeur doit être maximale pour une pièce strictement atonale ainsi que pour la musique aléatoire.

Les séquences musicales répertoriées chronologiquement dans le tableau I ont toutes été analysées en termes de critères de dimensionnalité et d’entropie ainsi que selon leur caractéristique spectrale ; les valeurs mesurées sont indiquées en regard des œuvres. La dernière colonne donne les résultats de la mesure de l’exposant v dans l’expression f^-v du spectre en fréquence (f) des séries temporelles de chaque pièce analysée. Pour la séquence de musique aléatoire, on obtient v = 0.01, c’est-à-dire pratiquement zéro, qui est la signature spectrale du bruit blanc. Les valeurs obtenues pour toutes les pièces musicales se situent dans le créneau 1.79 ≤ v ≤ 1.98 (voir le Tableau I ci-dessous) soit une valeur plus proche de celle du “bruit rouge” (v=2) que de celle du “bruit rose” (v=l).

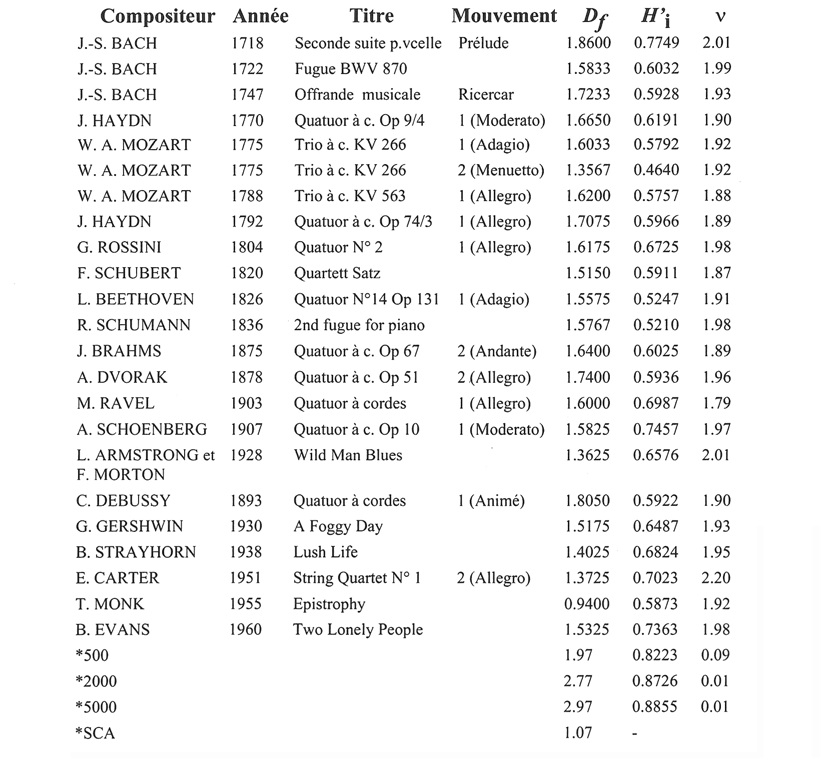
Tableau I : Les pièces marquées * ont été construites par ordinateur ; *500, *2000, *5000 sont des séquences de musique aléatoire ; *SCA est une gamme chromatique ascendante et descendante. Df est la dimension fractale de la trajectoire dans l’espace des phases, H’i est l’entropie paramétrée et v est l’exposant du spectre (~f-v) de la série temporelle.

Ce résultat semble à première vue en contradiction avec le comportement de type “universel” en 1/f. Mais cette “universalité” émerge de l’analyse spectrale de séquences de durées extrêmement longues (jusqu’à 24 heures) et sur de tels temps la théorie prévoit effectivement un spectre en 1/f. Cependant si l’analyse vise à identifier des éléments qui soient musicalement significatifs, l’entité à prendre en compte est la séquence que constitue une pièce unique, comme un mouvement en tant que tel. Le sens de la juxtaposition d’œuvres sur de longues durées demeure obscur du point de vue de la signification musicale.

Nous constatons que les valeurs de la dimension de la trajectoire dans l’espace des phases ainsi que celles de l’entropie paramétrée – notées respectivement D_f et H’_i dans le tableau I et la figure 4 – sont distribuées aléatoirement selon l’ordre chronologique des œuvres. Nous y reviendrons. Pour l’instant rappelons que D_f s’interprète comme une quantification de la dynamique globale et H’_i comme une mesure de la dynamique locale. Dans le graphique de la figure 4, nous avons porté le logarithme de D_f en fonction de celui de H’_i. S’il n’existait aucune corrélation entre ces deux grandeurs, les points se répartiraient de façon dispersée sur toute l’étendue du graphique. Au contraire, on assiste à une distribution confinée qui peut par ailleurs être ajustée par une cubique. Si aucune interprétation n’est susceptible de justifier cette forme analytique, il n’en reste pas moins que l’analyse fait apparaître une tendance qualitative, témoin de l’existence de corrélations entre la dynamique globale et la dynamique locale des œuvres musicales.

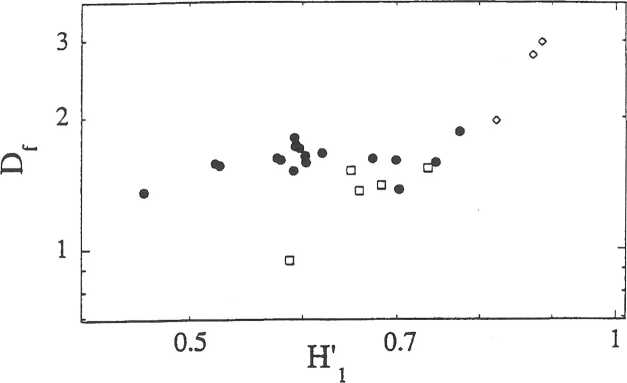
Figure 4 : Représentation logarithmique de la dimension fractale en fonction de l’entropie : logD_f = F (logH’₁). Différents symboles sont utilisés pour la musique classique (•), le jazz (□) et les séquences aléatoires (◊).

Nous avons émis la conjecture – du moins dans le cadre de la musique occidentale tonale – que les éléments sonores inattendus dans le déroulement d’une pièce de musique peuvent émerger des déviations par rapport aux règles d’écriture, de leur violation ou de leur rejet. Dans le contexte des formes classiques, ces déviations proviennent souvent de la liberté que le compositeur prend par rapport à la tonalité. Ainsi lorsque Leibowitz parle de la complexité du langage musical, il entend principalement celle qui résulte de l’audace du compositeur à rompre avec l’harmonie. Leibowitz avance une argumentation d’importance puisqu’elle le conduit à l’idée d’une complexité croissante qui déterminerait l’évolution historique de la tradition musicale. Si nous acceptons le concept physique selon lequel l’entropie constitue une mesure quantitative du degré de complexité, nous constatons que – contrairement à l’hypothèse de Leibowitz – la complexité apparaît comme une caractéristique spécifique de l’œuvre et non du compositeur. Dès lors l’idée d’un accroissement de la complexité dans l’écriture musicale parallèlement à l’évolution de la musique classique ne semble fondée sur aucune évidence.

La musique qui occupait une place quelque peu marginale dans le monde des phénomènes périodiques et des lois réversibles de la mécanique classique n’est plus aujourd’hui un corps étranger dans un univers instable, aléatoire et polarisé temporellement. La musique, selon Schopenhauer, est le reflet de lois fondamentales d’un univers qui incorpore naturellement le phénomène musical. Cette structure aléatoire, irréversible, nous la trouvons dans les manifestations phénoménologiques de la nature ; nous la trouvons aussi, selon des mécanismes dont nous ne comprenons pas encore très bien la signification, dans les phénomènes musicaux.

Que devient alors la notion de temps dans un univers irréversible et aléatoire ? Le concept selon lequel le temps rythme des évolutions périodiques est dépassé. Il faut introduire un temps qualitativement différent, un temps des changements, un temps qui se mesure par son contenu d’irréversibilité. Ce temps-là est très proche de celui qui sous-tend la musique où le temps de l’horloge n’a pas cours.