1. Introduction

Dès sa naissance il y a quatre milliards d’années, la matière vivante s’est munie de facultés étonnamment perfectionnées, par exemple la manipulation des symboles ou la construction de hiérarchies complexes. De toute évidence, ces facultés lui ont permis d’établir des systèmes stables et reproductibles dans un monde physique qui, au contraire, est dès l’abord instable et imprévisible. Pourtant, matière physique et matière vivante sont faites des mêmes atomes. Où réside la différence, comment comprendre cette fabuleuse divergence à partir des lois physiques que ces mêmes facultés nous ont fait découvrir ? Cet article tente d’affronter l’énigme en respectant les règles méthodologiques qui ont fait le succès des sciences exactes.

Selon ces sciences, l’univers se présente comme une grande hiérarchie de structures douées de deux propriétés générales : premièrement, les structures s’emboîtent sur trois axes issus du niveau moléculaire et s’étendant vers l’infiniment grand, l’infiniment petit et l’infiniment complexe ; deuxièmement, les structures interagissent par des influences caractéristiques des axes d’emboîtement. La physique a déjà identifié les interactions fondamentales intervenant sur les axes de l’infiniment petit et de l’infiniment grand : aux échelles extrêmes, elles prédominent en très petit nombre et elles conduisent à des dynamiques générales telles que mécanique classique, mécanique quantique ou thermodynamique (Cohen-Tannoudji 1994). En revanche, la science des systèmes n’a pas encore complètement élucidé les interactions qui couplent les structures complexes : à l’observateur qui y distingue nombre de niveaux d’organisation, les interactions semblent d’emblée multiples et compliquées, jugement qui décourage toute description générale du monde vivant. Cet article adopte la position opposée : pourvu que les observables élémentaires soient choisies au plus bas niveau de description, il s’avère que les interactions sont simples à la limite de l’infiniment complexe, et même formellement plus simples qu’en physique. Cette simplicité justifie la recherche d’une dynamique générale permettant en premier lieu de reconstruire les niveaux d’organisation qui ont fait problème.

La recherche repose cependant le problème épistémologique fondamental car l’observateur doit remonter aux définitions à la fois formelles et opérationnelles qu’exige la description de toute dynamique élémentaire (Pattee 1996). En effet, il n’existe aucune loi qui prédétermine les variables élémentaires, c’est-à-dire susceptibles d’organiser l’ensemble des données perçues. Le seul critère envisageable est qu’elles se prêtent à la formalisation dont l’observateur est capable ; par conséquent, il est réduit à découvrir ces variables par un acte mental de nature auto-référentielle. Quelle que soit la réalité envisagée, le premier problème est donc de découvrir des variables élémentaires appropriées, et d’énumérer ensuite les valeurs qu’elles prennent au cours des interactions : cette énumération implique une définition objective du temps comme variable indépendante supplémentaire. Le problème n’est nullement trivial en physique, mais une patiente observation a finalement mis en évidence les règles méthodologiques qui garantissent au mieux l’objectivité. Or, il est possible de mener l’observation selon les mêmes règles dans les systèmes très complexes ; il s’avère alors que les variables élémentaires certes différent de nature mais elles présentent des relations mutuelles analogues à celles reconnues en physique. En conséquence, la méthodologie s’applique à nouveau et elle garantit un standard d’objectivité comparable. Cette application a cependant un prix qui est d’introduire une nouvelle variable pour le temps, spécifique des systèmes complexes ; le gain est qu’un isomorphisme étendu se constitue entre physique et science des systèmes. L’isomorphisme est purement structurel et ne préjuge en rien de la nature des variables en jeu, mais il préserve toutes les opérations non-calculables de la mécanique statistique. Ainsi, il affranchit la science des systèmes du seul discours rationnel auquel elle est présentement réduite : en dictant des inférences originales que seule la physique justifie, il fournit d’abord une loi d’évolution intangible et valable pour tous les systèmes complexes ; ensuite, il ouvre des perspectives entièrement nouvelles pour expliquer les multiples ordres à longue portée qui prévalent dans ces systèmes.

Il est vrai que ce résultat va à l’encontre des idées reçues selon lesquelles les êtres vivants, et surtout leurs activités mentales, relèveraient d’un autre mode de description que les systèmes matériels. C’est la raison pour laquelle l’isomorphisme annoncé requiert la démonstration détaillée qui fait l’objet de cet article. En Sec. 2 et 3, la démonstration se fonde d’abord sur une définition objective du temps pour les particules de la physique classique, puis sur l’origine ergodique de la flèche du temps en thermodynamique. En Sec. 4 et 5, la même procédure conduit à une définition autonome du temps pour les composants des systèmes complexes ; il en ressort que si de tels composants s’adaptent ensemble à un contexte aléatoire figurant l’environnement naturel, une nouvelle flèche s’impose également pour ce temps autonome. La dynamique des systèmes relève alors d’une théorie ergodique analogue à la thermodynamique, et décrite en Sec. 6 sous le nom de morphodynamique. Il s’ensuit une série d’inférences selon lesquelles les systèmes complexes subissent des transformations irréversibles déterminant leurs échanges avec l’extérieur. En Sec. 7 sont particulièrement envisagés les échanges constituant des interactions de niveau supérieur avec d’autres systèmes de complexité comparable. A ce niveau, la théorie s’assortit d’une interprétation cognitiviste où ces interactions forment une nouvelle classe : elles ont un contenu symbolique qui participe à la construction des représentations dans des échelles de temps spécifiques des systèmes mentaux. Ainsi, la théorie est à même de traiter au plus haut niveau les activités d’apprentissage et d’invention des personnes, ainsi que les activités collectives qui président à l’effort de civilisation.

2. Dynamique des particules physiques

Même si l’on se borne à la dynamique classique, l’établissement de lois objectives n’est pas trivial car non seulement l’observation des variables est difficile mais l’observateur ne peut compter sur ses états mentaux pour définir ces variables. Par exemple, Newton considérait comme évident que le temps s’écoule spontanément à un taux invariant avec les événements ; cette conjecture correspond à l’impression mentale de certains observateurs, mais elle ne relève en rien de phénomènes physiques indépendants d’eux. En particulier, la mesure des vitesses exige de comparer des intervalles spatiaux ou temporels qui ne se recouvrent pas ; or, la comparaison fait intervenir la mémoire qui consiste en reconstructions mentales subjectives et dépendantes de l’histoire des personnes. En revanche, des constats de coïncidence entre paires d’événements survenant simultanément et au même endroit sont des perceptions ponctuelles qui ne font pas intervenir les représentations antérieures. Par conséquent, la connaissance objective peut légitimement s’appuyer sur de tels constats de coïncidence. Sur cette base plus restrictive, la procédure d’observation et de formalisation de la dynamique d’un objet physique peut par exemple se dérouler comme décrit ci-dessous.

L’espace est d’abord défini comme l’extension perceptible par l’observateur et dans laquelle l’objet observé se déplace. Les lieux de l’extension sont repérables à l’aide de règles matérielles mises bout à bout dans trois directions perpendiculaires ; ensuite, la coïncidence observée entre objet et règles mesure les trois dimensions de sa position. Ce repérage présume que les règles gardent une longueur fixe au cours de la manipulation, contrainte dont la compatibilité avec les phénomènes physiques exige vérification expérimentale. De plus, le repérage requiert le choix préliminaire de l’origine et de l’orientation des directions. Ce choix définit le référentiel de mesure, instrument de description a priori arbitraire : l’observateur doit aussi le présumer soumis à une contrainte de nature physique à déterminer par l’expérience.

Le temps est ensuite défini comme l’extension continue perceptible par l’observateur lorsqu’il voit l’objet occuper successivement des positions différentes dans l’espace. Ce “temps perçu” est à définir comme une quatrième variable indépendante avec un statut particulier : elle paraît analogue à une dimension de l’espace mais il subsiste deux différences capitales qui interdisent la définition par analogie. D’une part, l’extension est manifestement parcourable dans un seul sens, asymétrie absente dans l’espace ; d’autre part, il n’existe pas d’instrument matériel manipulable à la manière des règles dans l’espace (les horloges font intervenir des phénomènes dépendant du temps et leur usage suppose que la dynamique est déjà connue). Tant la définition que la mesure du temps restent donc a priori arbitraires, et l’observateur doit également présumer ces arbitraires soumis à des contraintes de nature physique à déterminer. A ce stade, la perception du mouvement ne fournit qu’un seul renseignement, à savoir que les trois dimensions de la position de l’objet sont des variables dynamiques qui varient avec le “temps perçu”. Pour accéder aux définitions objectives et opératoires qui se substitueront aux présomptions, l’observateur doit conduire quatre expériences de physique et en formuler les résultats sous forme mathématique (pour simplifier, seul le cas unidimensionnel est traité ci-dessous) :

Expérience 1. Mouvement en l’absence de cause. Lorsque l’objet isolé, c’est-à-dire assez éloigné de tout autre qui l’influence, se déplace d’un lieu initial au lieu final plus éloigné de Δx, on observe dans certains référentiels que l’objet parcourt des distances égales pour des accroissements égaux du “temps perçu” Δt :

(2.1) Δx = νΔt

Donc la vitesse v est présumée constante dans le cas de l’objet isolé dans les référentiels de mesure que les expériences suivantes doivent définir.

Expérience 2. Mouvement en présence d’interaction localisée avec un autre objet. On observe que v n’est plus constant ; au contraire, il varie fortement dans le “temps perçu”, et l’autre objet est source du changement par l’intermédiaire d’une force dépendant de la position, F (x). A la limite (sphères dures), la force est très grande sur une durée très petite et la variation Δv est discontinue. On observe que tant que les deux objets interagissent, les variations Δv de chacun sont interdépendantes : elles sont de signe opposé et inversement proportionnelles à la quantité de matière m, qui est un paramètre constant durant le mouvement. Par conséquent, la variation composite Δp = mΔv est indépendante de l’objet, et elle change avec le “temps perçu” alors que la somme sur les deux objets reste nulle et invariante pendant toute la durée de l’interaction. Ces observations sont consignées dans les relations :

(2.2) Δp = F₁₂ Δt, F₁₂ = –F₂₁

où les indices distinguent les forces exercées par le deuxième objet sur le premier et réciproquement. La nouvelle variable dynamique est appelée quantité de mouvement p ; rapportée au volume, elle représente plus précisément un flux temporel de matière, soit la quantité de matière traversant une surface unité en un temps unité. La quantité de mouvement a l’avantage d’être plus générale que la vitesse et de donner lieu à des équations dynamiques plus symétriques. En effet, passant à des accroissements infinitésimaux, on obtient le système d’équations différentielles couplées :

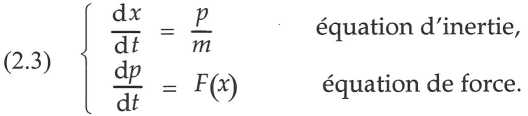
A partir de ces équations, on calcule le temps écoulé en fonction de la distance parcourue en faisant le rapport des deux variables dynamiques x et p :

La quantité de mouvement s’exprime en fonction de la position par l’élimination de la variable t entre les Éq. (2.3) ; il en résulte l’intégrale première interprétée comme conservation de l’énergie :

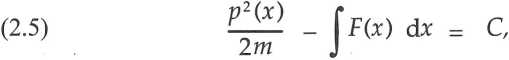
avec C une constante arbitraire. Comme les Éq. (2.4) et (2.5) ne font intervenir que la variable x qui est présumée directement observable, elles constituent la définition opérationnelle du temps en physique.

Expérience 3. Mouvement en présence d’interaction attractive et fonction linéaire de la distance :

(2.6) F(x) = – k(x)

avec k un paramètre constant durant le mouvement. Par substitution et élimination de p dans les Éq. (2.3), on calcule ce mouvement :

Le calcul prévoit un mouvement stable et périodique : l’amplitude du mouvement A est une constante dans le “temps perçu”, et la période τ, tirée de la solution ci-dessus ou directement des Éq. (2.4-5), est une constante indépendante de la nature des variables choisies x et p ; elle est fixée par les seuls paramètres constants :

Expérience 4. Vérification expérimentale du mouvement de l’objet isolé : La force décrite par l’Éq. (2.6) est réalisable expérimentalement en liant par exemple l’objet de masse m à un ressort de constante élastique k de façon à constituer un système oscillateur. L’expérience fournit ainsi les étalons de longueur et de temps pour les variables x et t introduites dans les Éq. (2.3) : bien que ces étalons ne soient pas absolus, ils permettent à l’observateur de contrô1er que les règles restent de longueur constante et de mesurer la variable temps en unités de la période : il utilise alors l’oscillateur comme horloge de façon analogue à l’usage des règles pour mesurer l’espace. Il peut enfin constater par mesure directe que, dans le référentiel choisi, l’objet isolé parcourt bien des distances égales pendant les périodes successives de l’oscillateur. Il détient ainsi un test physique autorisant la mesure de x dans ce référentiel, ou d’autres dits “inertiels” : ils sont tels que tout objet isolé y garde une vitesse invariante dans le temps. Enfin, l’expérience de l’oscillateur confirme la stabilité du mouvement dans ces référentiels, ainsi que la dépendance de la période dans les paramètres constants m et k.

A ce point, toutes les présomptions nécessaires pour établir la dynamique de l’objet physique se trouvent vérifiées par l’expérience. L’observateur acquiert ainsi le résultat formel recherché : une fonction linéaire d’une variable mathématique t représente exactement l’écoulement spontané du temps en physique classique, à condition toutefois que les équations dynamiques décrivent le mouvement dans les référentiels autorisés. Pour l’espace comme pour le temps, définition et mesure se basent seulement sur des phénomènes physiques qui se déroulent sans interférence de la part de l’observateur, et qui sont reproductibles par tous les autres observateurs. Définition et mesure des variables sont donc objectives au sens faible, c’est-à-dire communes à la plupart des observateurs compétents, et elles sont acceptables pour représenter la réalité au travers des Éq. (2.3). En conclusion, les variables dynamiques conjuguées x et p, la source de changement F et la variable temps t sont identifiées comme quatre grandeurs a priori indépendantes mais codéterminées opérationnellement par l’intermédiaire des équations dynamiques. Ces équations sont immuables et universelles, et elles ont le pouvoir de donner un sens physique objectif à toutes les variables présumées à partir de l’observation, y compris le temps (Jacob 1994).

La même démarche devrait en principe être répétée pour les dynamiques indépendantes de la mécanique classique, par exemple l’électrodynamique ; on trouverait alors que la variable temps y garde les mêmes propriétés et qu’elle est donc commune à tous les phénomènes physiques répertoriés. Cependant, la nature exacte du temps fait encore problème. En effet, l’observateur a constaté que le “temps perçu” est parcourable dans un seul sens, alors que les équations dynamiques ne distinguent pas le sens de parcours : les trajectoires prédites sont invariantes par renversement du temps. Le temps aurait donc la propriété d’être réversible en physique mais cette propriété n’est jamais observée. De ce fait, elle est inaccessible à la conscience, bien qu’on puisse s’en donner une image artificielle en visionnant un film : que le sens de déroulement du film soit correct ou non, le mouvement de l’oscillateur garde la même apparence et l’observation ne permet effectivement pas de le décider. Il reste que l’expérience confirme que les équations dynamiques reproduisent fidèlement le mouvement des objets physiques dans des circonstances très diverses. Il faut par conséquent les accepter telles quelles, y compris la différence d’avec la perception.

L’observateur peut choisir de donner à cette différence une raison physique ou une raison perceptuelle. La raison physique serait que le temps s’écoule bien dans l’unique sens indiqué par la perception, de sorte que les solutions mathématiques inversées sont à écarter car dépourvues de signification physique. La raison perceptuelle serait que l’irréversibilité apparaît comme un problème d’objectivité : elle naît au cours de la perception par laquelle l’observateur humain adapte ses états mentaux à l’événement physique ; dans ce cas, le sens inversé ne lui est pas connaissable et il doit être écarté car dépourvu d’utilité opératoire pour ce type d’observateur. Les observations faites seulement en mécanique classique ne permettent pas de trancher entre ces deux raisons, mais la dynamique des systèmes lèvera l’ambiguïté plus loin.

Le résultat essentiel est que cette description dynamique confère un nouveau statut à l’espace-temps. Au lieu d’être l’unique intuition a priori dans laquelle nous puissions percevoir la réalité (Petitot 1992, p. 40), il apparaît plutôt comme une notion non-observable et construite à dessein : nous construisons l’espace-temps parce que nous croyons a priori que nous pouvons formaliser tout ou partie des données perçues. Cette croyance est la réponse mentale au destin universel des êtres vivants : ils doivent tous s’adapter à un monde imprévisible. Comme on le verra plus loin, les croyances font partie des stratégies d’adaptation supérieures, et elles sont auto-référentielles car elles tiennent autant de l’observateur que des réalités qu’il tente de formaliser. Les notions non-observables ainsi construites ne sont donc pas nécessairement uniques et elles peuvent changer de nature lorsqu’il passe d’une réalité à l’autre, par exemple celle des objets physiques et celle des êtres vivants. Il lui reste donc à rechercher ces notions nonobservables en prenant conscience de toutes les ressemblances et différences que les sens et l’intelligence peuvent attester en face de ces diverses réalités.

3. Dynamique des systèmes physiques

La dynamique des systèmes se déduit de celle des particules en tenant compte qu’ils consistent en de nombreuses particules en interaction permanente par paires. Les interactions dépendent des positions relatives des particules de sorte que pour la particule d’indice i, les équations dynamiques sont :

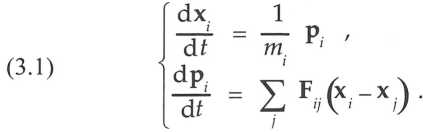
Pour une paire de particules i et j dans l’espace à trois dimensions, on sait que la dynamique se ramène à quatre équations de conservation pour l’énergie et les composantes de la quantité de mouvement ; or, le problème compte six inconnues qui sont les composantes des deux vitesses après l’interaction. La dynamique ne définit donc pas entièrement le problème et la prévision requiert un renseignement supplémentaire, à savoir un modèle formel de l’interaction. Le modèle le plus simple que suggère l’expérience est celui qui représente les particules comme des sphères dures entre lesquelles les forces d’interaction sont répulsives et normales aux surfaces au point de contact. Le problème est alors entièrement défini, mais il est renouvelé par la nature particulière des forces : parce qu’elles sont non-linéaires, elles donnent nécessairement lieu à un chaos déterministe par amplification des déviations (Schuster 1984). Or, pour déterminer physiquement les vitesses initiales, des interactions préalables avec d’autres particules sont indispensables ; par exemple, un “canon à particules” fixe la vitesse d’éjection par contacts répétés avec les particules des parois. Les vitesses d’entrée dans une collision contiennent donc toujours des déviations non-connaissables qui sont ensuite amplifiées au cours du phénomène. Pour ces raisons, les vitesses de sortie des collisions ne sont pas complètement prévisibles par les équations de la dynamique même lorsque l’interaction est connue.

Selon les Éq. (3.1), de telles interactions de paires se répètent un très grand nombre de fois dans un système de plusieurs particules ; elles rendent à terme les trajectoires chaotiques quelles que soient les conditions initiales pour les particules individuelles. Ce caractère chaotique justifie l’hypothèse ergodique selon laquelle la moyenne de toute variable prise sur le temps tend vers une valeur constante égale à la moyenne spatiale. Le système tend alors nécessairement vers un état d’équilibre thermodynamique. Il est caractérisé par un paramètre macroscopique, la température, mesurant la moyenne de l’énergie cinétique des particules. Quels que soient les mécanismes qui redistribuent cette énergie lors des collisions, la thermodynamique établit que les états d’équilibre satisfont deux principes globaux : l’énergie totale est conservée et l’entropie est maximalisée. Ce résultat permet de calculer les états d’équilibre lorsque particules et interactions sont connues, ainsi que les quantités d’énergie que les systèmes peuvent échanger par couplage mutuel.

L’évolution est par conséquent nécessaire et spontanée, mais elle est lente car de nombreuses interactions successives sont nécessaires pour répartir les perturbations locales sur tout le volume du système : la tendance est manifeste après que le temps s’est suffisamment écoulé. Ainsi, l’évolution vers le chaos s’observe toujours dans le sens “positif’ d’écoulement du temps, alors qu’une évolution spontanée vers un ordre accru ne s’observe jamais. Cette asymétrie est souvent désignée comme la “flèche du temps thermodynamique” : en nombre suffisant, les phénomènes d’interaction désignent le sens positif bien que leur dynamique individuelle ne fasse aucune distinction quant au sens du temps. Cette propriété d’irréversibilité est caractéristique du comportement ergodique : il n’exclut pas qu’un mouvement exactement inverse se produise, mais c’est une éventualité parmi d’autres en nombre si grand qu’on peut le qualifier d’invraisemblable à toutes fins pratiques. Le comportement ergodique relève ainsi d’une loi de nature statistique s’appliquant aux conditions initiales des interactions, et stipulant qu’elles contiennent toujours des déviations en raison même des processus physiques qui les déterminent. Cette loi est donc étrangère aux lois dynamiques des particules isolées, mais elle doit leur être ajoutée pour décrire complètement la réalité des systèmes de plusieurs particules. On a d’ailleurs proposé de l’affirmer comme “principe cosmologique” indépendant (Layzer 1990) bien qu’elle se déduise de processus physiques clairement identifiés.

Le sens positif d’écoulement du temps est aussi le seul sens détecté par les instruments de mesure du laboratoire : par exemple, les horloges sont basées sur des cycles réversibles, mais elles comprennent toujours un échappement, mécanisme irréversible capable de sommer les cycles accomplis. De façon générale, les instruments de mesure font nécessairement intervenir des processus macroscopiques irréversibles lorsqu’ils convertissent la grandeur mesurée en signal déchiffrable par l’observateur. La contradiction entre réversibilité de la dynamique et irréversibilité de l’observation n’est donc qu’apparente : la dynamique à elle seule ne suffit pas à décrire l’observation des grands systèmes. Ce “problème de la mesure” a suscité beaucoup de discussions en mécanique quantique, mais il se pose de manière analogue déjà en mécanique classique (Prigogine et al. 1979).

Enfin, le sens positif d’écoulement du temps est aussi le seul sens perceptible par la conscience : l’écoulement dans le sens négatif lui est inconcevable. La physique des systèmes non-linéaires suggère ainsi un modèle d’irréversibilité qui pourrait s’appliquer à la conceptualisation du temps. Il convient cependant de démontrer d’abord que les processus mentaux se fondent aussi sur des comportements ergodiques.

4. Dynamique des structures fonctionnelles

Dans cette démonstration, il faut reconnaître d’emblée que les variables identifiées en physique ne conviennent pas pour les systèmes vivants : les éléments qui les composent ne sont certainement pas décrits par des variables du type position ou quantité de mouvement. Leur dynamique est donc irréductiblement différente, de sorte que le temps opérationnellement défini et mesuré en physique comme rapport de ces variables ne peut garder la même signification. Pour déterminer la signification qu’il prend pour les être vivants, il faut d’abord rechercher les variables appropriées aux changements particuliers qu’ils donnent à observer comme systèmes composés de nombreux éléments. Ensuite seulement, la physique se révélera le modèle adéquat pour construire une dynamique par analogie.

Suivant cette idée, on présume d’abord que les changements dans les systèmes vivants s’expriment par des variables dynamiques caractérisant leurs éléments ; on présume ensuite que ces variables dépendent d’un “temps spécifique” de la dynamique des éléments. Il n’y a pas de raison a priori pour que ce temps soit identique ni au “temps perçu” par la conscience de l’observateur ni au temps mesuré par les horloges physiques. Tout au plus, l’analogie suggère que les variables dynamiques se présentent par paires : l’une x représente une configuration spatiale et l’autre p représente un flux temporel ; de cette façon, leur rapport constituera la définition opérationnelle de la variable “temps spécifique” t à la manière de l’Éq. (2.4). Si l’analogie se vérifie, les observations sur les éléments des systèmes vivants conduiront au même résultat qu’en physique : elles parviendront à identifier à la fois deux variables appropriées, le temps spécifique et la source de leurs changements.

Pour procéder à cette identification, on admet que la dualité structure-fonction est fondamentale pour décrire les éléments des systèmes vivants capables d’adaptation. La description explicite est qu’un système vivant se compose d’éléments appelés structures fonctionnelles. Chaque structure fonctionnelle contient des particules matérielles en grand nombre et constitue un sous-système physique non-linéaire et ouvert, et donc régi par les principes de la thermodynamique loin de l’équilibre ; en particulier, le sous-système peut transiter entre deux structures stables et il produit une fonction particulière à des taux nettement différents dans chacune d’elles. La capacité d’adaptation s’énonce déjà au niveau de la structure fonctionnelle car celle-ci est concevable comme conditionnellement adaptative : suivant l’état interne, elle reste fixe ou transite à l’autre état ; dans ce dernier cas, une influence externe a dépassé un certain seuil, et la fonction change en guise de réponse adaptative à cette influence.

Pour formaliser ces descriptions, la première variable appropriée x est celle qui repère la structure momentanée du sous-système, c’est-à-dire le paramètre d’ordre d’un système physique à dynamique de bifurcation ; la deuxième variable est le débit fonctionnel p dans la structure repérée, c’est-à-dire la quantité d’énergie-matière traitée par unité du “temps spécifique”. Enfin, ce temps t et l’influence externe I confèrent les propriétés énoncées si les variables obéissent les deux équations dynamiques couplées suivantes (Fivaz 1993) :

avec D et K des constantes caractéristiques du sous-système. En effet, la première équation représente une dynamique de bifurcation développée en fronce autour de la singularité (Thom 1974) ; cette dynamique implique que le paramètre externe I soit invariant avec x et ne dépende que de p. Dans ces conditions, la structure change conditionnellement d’état selon la valeur de la constante D : si D est négatif, la variable de configuration x reste pratiquement invariante, mais si D est positif, elle transite entre ses deux déterminations stables lorsque le paramètre I (p) atteint en valeur absolue la valeur critique :

(4.2) I_c = √4 D³ / 27.

D a donc valeur de seuil de sensibilité à l’influence extérieure I. La deuxième équation affirme que, après la transition de x, la fonction associée p croît dans le “temps spécifique” au taux caractérisé par la constante K définie positive. Cette constante évalue donc un niveau de performance de la structure, et la paire D et K caractérise visiblement un élément de l’appareil sensori-moteur d’un système vivant. Lorsqu’un tel système est isolé, cependant, certaines fonctions restent actives afin d’assurer le métabolisme de base ; or, les équations décrivent les variations par rapport à cet état de référence qui fait l’objet de contraintes biologiques à identifier par l’expérience : on voit donc l’état de référence jouer ici le même rôle que le référentiel de mesure en physique.

Suivant la définition établie par l’Éq. (2.4) pour les équations de la physique, on calcule le “temps spécifique” écoulé en fonction du débit fonctionnel en faisant le rapport entre les variables dynamiques. Il s’agit donc du rapport du débit fonctionnel au paramètre d’ordre :

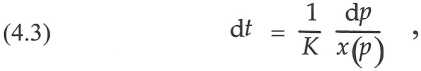
rapport qui reprend le rôle de définition opérationnelle du “temps spécifique” dans les systèmes complexes. Le calcul se simplifie si D est assez grand, car alors le paramètre d’ordre suit de près la trajectoire d’équilibre de la fronce où il reste stationnaire :

(4.4) x³ – Dx = I(p),

avec la solution approchée x(I) = ±√D pour – I_c 〈I 〈 I_c. En fin, on considère le cas particulier où le terme de couplage est linéaire et attractif,

(4.5) I(p) = – υp,

avec v une troisième constante du sous-système. Dans ce cas, les Éq. (4.1) décrivent un mouvement périodique comme en physique : la structure accomplit un cycle d’hystérèse (cycle limite) où les segments sur la trajectoire d’une détermination se terminent par la transition à l’autre détermination lorsque I atteint les valeurs critiques de l’Éq. (4.2). La période du cycle s’obtient par intégration de l’Éq. (4.3) entre les limites p- et p + correspondant aux deux valeurs critiques ± Ic :

Avec le changement de variable p = I/v et la solution approchée de l’Éq. (4.4), la période du cycle vaut :

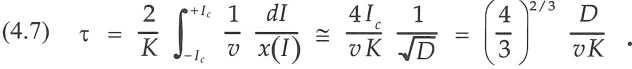
La période est ainsi fixée par les trois constantes propres du sous-système et elle est indépendante de l’observateur comme en physique : l’élément ainsi décrit peut donc aussi servir d’horloge. Si la confrontation avec l’expérience est positive, on pourra conclure que des structures fonctionnelles existent avec une dynamique reliant quatre variables a priori indépendantes : les variables dynamiques x et p, la source de changement I et le temps spécifique t sont codéterminées opérationnellement par l’intermédiaire des Éq. (4.1). De plus, ces grandeurs s’avèrent toutes mesurables sans aucune référence aux phénomènes physiques sous-jacents.

Or, l’expérience foisonne de preuves : la plupart des êtres vivants sont pourvus d’horloges biologiques (Winfree 1987). Les plus communes sont les horloges circadiennes oscillant sur des cycles limites au niveau cellulaire, tandis que d’autres horloges fonctionnent à des niveaux plus élevés où plusieurs organes interagissent, par exemple les cycles hormonaux. Les horloges biologiques sont réglables et synchronisables sur signaux externes selon des principes analogues aux horloges physiques, mais la physiologie détaillée n’est pas connue. Le neurone et le pouls cardiaque sont les exemples classiques de systèmes à cycles limites parcourus sur signal externe. Mathématiquement, les équations proposées pour décrire leur dynamique ont précisément la même structure que les Éq. (4.1) et (4.5) : pour le neurone, la paire de variables dynamiques comprend la polarité électrique et le courant de décharge, tandis que pour le système cardiaque, les variables considérées sont l’élongation des fibres musculaires et un potentiel électrochimique contrôlant la diffusion à travers la membrane musculaire (Zeeman 1972).

Il existe également de nombreux systèmes abstraits qui accomplissent des cycles répétés et souvent hiérarchisés dans un même système. Par exemple, on peut citer les rythmes et mélodies musicales (Bamberger 1991), le chant canon et le contrepoint (Hofstadter 1979), les textes scandés et versifiés, les tours de parole des conversations (Jaffe et al. 1970), les cycles historiques et économiques, etc. Pour ces systèmes abstraits et très complexes, il est vrai que les variables dynamiques appropriées restent souvent à identifier. Néanmoins, l’existence même de ces multiples horloges atteste la pertinence des équations envisagées pour la dynamique à des niveaux de complexité très divers : le nombre des variables par composant est plus petit qu’en physique, et les interactions sont même plus simples puisqu’elles sont unidimensionnelles. Les horloges prouvent subsidiairement que les composants des systèmes complexes évoluent dans un temps autonome, c’est-à-dire sans lien direct avec les processus physiques sous-jacents. Les périodes résultent donc de l’organisation complexe exclusivement. Cependant, puisque ces périodes s’avèrent constantes à moyen terme, il est justifié de les classer à l’aide d’horloges physiques comme on le fait en pratique.

En conséquence, on voit le temps revêtir la même signification générale du point de vue opérationnel, à savoir le rapport existant entre flux temporels et variables de configuration. Ces grandeurs présentent donc les mêmes relations logiques dans les systèmes physiques et dans les systèmes biologiques, mais elles gardent des différences de nature irréductibles qui disqualifient toute analogie directe. En particulier, la comparaison des Éq. (2.3) et (4.1) montre que les rôles dynamiques des variables de configuration et des flux sont croisés : alors que les positions sont continues et les quantités de mouvement souvent discontinues en physique, la dynamique des systèmes complexes désigne les flux comme continus et les variables de configuration comme éventuellement discontinues. Ce croisement est la marque distinctive qui ressort de la confrontation entre le temps dans les systèmes physiques et le temps dans les systèmes biologiques ; ses conséquences vont se répercuter dans toutes les correspondances envisageables entre ces systèmes.

Ce point clairement établi, on peut rappeler que la forme des équations dynamiques satisfait des contraintes à la fois biologiques et physiques. La première des Éq. (4.1) est la plus simple qui rende compte de la capacité d’adaptation des structures fonctionnelles, donnée biologique qui est dépourvue de nécessité physique. Par contre, la forme de la deuxième des Éq. (4.1) est imposée par la physique : comme les structures fonctionnelles sont des systèmes physiques ouverts, les flux s’établissent progressivement dans le temps car les particules physiques doivent s’accélérer sous l’action des forces disponibles. Par exemple, la version linéaire de la thermodynamique des processus irréversibles relie les flux aux forces généralisées par des équations non-homogènes de type Boltzmann ; leurs solutions ont un temps de relaxation fini, et les valeurs d’équilibre sont caractérisées par les constantes soumises aux relations de Onsager (Fivaz 1994). Les Éq. (4.1) négligent toutefois les effets de relaxation car elles ont ici pour but premier de décrire comment les flux évoluent immédiatement après les transitions des variables de configuration.

5. Dynamique des systèmes complexes

Cette dynamique constitue la morphodynamique au sens strict qui se base sur les trois hypothèses constructives suivantes :

1) Le système complexe est un ensemble de N structures fonctionnelles définies par les Éq. (4.1). L’ensemble est supposé complet et fermé dans le sens qu’il assure toutes les fonctions nécessaires et qu’il n’échange pas ses éléments avec l’extérieur. Ces conditions définissent les systèmes dits autopoïétiques : les structures fonctionnelles restent en nombre fixe et concourent à l’activité globale de façon auto-cohérente. Ainsi, chaque structure remplit tout ou partie d’une des fonctions nécessaires, et chaque fonction contribue au maintien d’une ou plusieurs des structures présentes. Par exemple, les êtres vivants se maintiennent d’eux-mêmes sans échanger de cellules fonctionnelles avec l’extérieur ; de même, le cerveau opère sans exporter ou importer des neurones.

2) Les structures fonctionnelles sont en interaction mutuelle par l’intermédiaire de leurs flux fonctionnels. Les interactions peuvent être soit répulsives, c’est-à-dire empêchant que deux structures en interaction remplissent la même fonction, soit attractives, c’est-à-dire associant les structures dont les fonctions se complètent ou s’enchaînent : la biologie et l’économie désignent couramment ces interactions par compétition et coalition.

3) Les structures fonctionnelles sont couplées à des paramètres extérieurs aléatoires, c’est-à-dire constants dans le court terme mais sans coordination dans le long terme.

Ces trois hypothèses sont formalisées dans un système de 2N équations dynamiques qui ont pour la structure d’indice i la forme suivante :

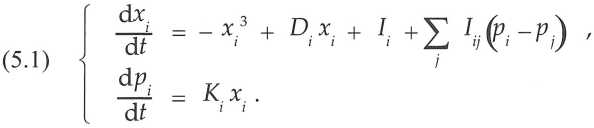
Comme les variables sont unidimensionnelles, les interactions mutuelles Iij ne produisent pas le chaos endogène trouvé dans le cas tridimensionnel de la physique. En revanche, le terme d’influence externe Ii est aléatoire et constitue la source de chaos exogène affectant les variables microscopiques. Leur comportement est donc analogue à l’agitation thermique qui règne dans les systèmes thermodynamiques, et il justifie que l’hypothèse ergodique s’applique avec les mêmes conséquences macroscopiques : les systèmes complexes subissent une évolution nécessaire et spontanée vers un état d’équilibre à long terme. Cet état est nommé équilibre morphodynamique pour rappeler que les grandeurs redistribuées au hasard sont des paramètres d’ordre au lieu des quantités de mouvement thermalisées en thermodynamique. A cette substitution près, un isomorphisme complet se présente avec les théories physiques comprenant la mécanique classique, la thermodynamique et la mécanique statistique. Ainsi comme en physique, une tendance vers l’équilibre s’observe dans le sens positif du temps seulement. Le sens est privilégié au niveau système : la même propriété d’irréversibilité réapparaît comme conséquence du comportement ergodique. La seule différence concerne l’origine du chaos déterministe induisant ce comportement. Alors que les interactions internes y pourvoient en physique, des interactions non-linéaires à l’extérieur du système complexe sont indispensables : elles produisent le chaos déterministe supprimant toute corrélation entre les influences externes. Dans le système complexe, le comportement ergodique reflète donc les activités incoordonnées de tous les autres systèmes déjà présents l’environnement naturel.

Cependant, contrairement à la physique où la dynamique est exactement réversible, les structures fonctionnelles présentent des effets d’hystérèse irréversibles. Ils sont de l’ordre de Ic, mais cette limite est petite comparée aux grandes influences externes I qui entretiennent l’activité dans les systèmes complexes. Par ailleurs, la matière vivante a la capacité de restaurer exactement les états initiaux de ses structures après chacune de leurs transitions. Il en résulte que toute configuration momentanée est accessible de n’importe quelle autre avec la même probabilité et indépendamment des configurations précédentes. Cette condition, qui est nécessaire pour que l’équilibre s’établisse, est donc satisfaite tout comme en physique où la condition équivalente, dite de balance détaillée, résulte de la réversibilité dans le temps. Ainsi, malgré l’hystérèse, les structures de la matière vivante se comportent comme si leur dynamique était exactement réversible.

Dès lors et de même qu’en thermodynamique, la réversibilité disparaît au niveau des systèmes réels qui comptent un grand nombre de structures en interaction : ils accèdent spontanément et irréversiblement à des états stationnaires, et un petit nombre de variables macroscopiques suffit à les décrire complètement. La principale, appelée température complexe, mesure le niveau de l’activité stochastique ; elle a donc les mêmes propriétés que la température ordinaire dans les systèmes physiques. Cette grandeur est proportionnelle à une fonction des paramètres apparaissant dans les Éq. (5.1) :

Dans cette expression, les crochets représentent la prise de moyenne sur l’ensemble des structures fonctionnelles du système. La température complexe est d’autant plus grande que ces structures sont plus sensibles et performantes : l’interprétation par les mérites de l’appareil sensori-moteur est évidente. En outre, l’existence de l’équilibre conduit à des principes dynamiques qui s’appliquent à des grandeurs spécifiques aux systèmes complexes : ils en gouvernent l’évolution lors de transformations par échanges avec l’extérieur. L’isomorphisme suggère donc d’identifier les grandeurs macroscopiques qui correspondent aux grandeurs d’intérêt en thermodynamique : en premier lieu, les systèmes physiques ont deux modalités d’échange sous forme de travail et de chaleur ; en deuxième lieu, les principes régissent des fonctions d’état qui sont l’énergie et l’entropie. Ces identifications doivent impérativement tenir compte des quatre critères suivants :

a) la logique et les relations établies en thermodynamique entre les variables des niveaux microscopique et macroscopique ;

b) le caractère ordonné ou non des échanges selon la thermodynamique ;

c) la nature spécifique des variables dynamiques dans les systèmes complexes ;

d) le croisement des rôles des variables dynamiques par rapport à la physique.

6. La morphodynamique

Avec les précautions indiquées, l’isomorphisme avec la physique conduit à plusieurs propriétés des systèmes complexes qui sont indémontrables par d’autres moyens. En effet, si les critères ne déterminent peut-être pas uniquement toutes les identifications admissibles, la cohérence que ces identifications doivent garder entre elles impose au moins la série d’inférences suivantes :

Inférence 1. Selon la thermodynamique, le travail est l’échange ordonné au cours duquel un domaine de positions est cédé par l’un des partenaires au profit de l’autre. En morphodynamique, l’échange correspondant porte sur un ensemble de fonctions qu’un système cède au système partenaire : l’ensemble constitue donc un comportement exécuté en faveur du partenaire ou, en d’autres termes, un service qui lui est rendu et qui le dispense d’exécuter les fonctions en question.

Inférence 2. Selon la thermodynamique, l’échange de chaleur est désordonné et transfère l’amplitude des mouvements des particules sans céder les positions. En morphodynamique, l’échange correspondant doit transférer des valeurs de paramètres d’ordre sans céder les fonctions associées : le jeu de valeurs échangées constitue donc une suite non-prévisible de symboles qui figure un comportement complexe sans que celui-ci soit exécuté. En d’autres termes, il s’agit d’un message qui encode un comportement de l’émetteur, et le récepteur peut ensuite le décoder en un comportement propre.

Inférence 3. Selon le premier principe de la thermodynamique, chaleur et travail sont sommables et leur somme est la fonction d’état dite énergie interne ; cette fonction est conservée dans toute transformation cyclique d’un système. En morphodynamique, le principe correspondant affirme que comportements et messages sont sommables, et par conséquent mesurés par des valeurs dont la somme est une fonction d’état. Cette fonction est conservée dans toute transformation cyclique d’un système complexe, c’est-à-dire que comportements et messages ont des valeurs qui s’échangent sans gain ni perte. L’exemple économique de telles valeurs est le prix convenu lorsqu’une personne échange son travail contre une somme d’argent. La fonction d’état représente donc une forme de propriété interne du système qui a les mêmes propriétés formelles que l’énergie en physique. Elle couvre à la fois les biens réels issus de son activité et les biens immatériels exprimables par des symboles tels que monnaie ou connaissance.

Inférence 4. Selon le deuxième principe de la thermodynamique, les transformations entre travail et chaleur sont asymétriques et irréversibles, de sorte que l’entropie d’un système thermiquement isolé ne peut que croître. En morphodynamique, le principe correspondant affirme l’existence d’une nouvelle fonction d’état : elle est nécessairement croissante dans les transformations d’un système isolé, ce terme signifiant que le système est privé de tout message extérieur. Cette fonction, appelée complexité, est maximale lorsque le système atteint l’état d’équilibre. Elle mesure le nombre de configurations que peuvent prendre les paramètres d’ordre et les fonctions ; elle est donc analogue à l’entropie qui mesure le nombre de configurations des positions et des vitesses des particules physiques.

Inférence 5. Selon la thermodynamique, un système accède à l’ordre interne par transition de phase, phénomène au cours duquel un flux d’entropie s’évacue par contact avec un environnement plus froid. Par exemple, un gaz condense ou cristallise quand la chaleur dite “latente” est déplacée vers un domaine spatial à température plus basse. En morphodynamique, le phénomène correspondant est l’émergence d’ordre interne, mais il faut que le système soit en contact avec un environnement à température complexe plus basse. La différence capitale d’avec la physique provient du croisement des rôles des variables : l’ordre dans le système complexe apparaît comme paramètre d’ordre de l’espace fonctionnel et non de l’espace de configuration comme en physique. Il ne se manifeste donc pas comme arrangement géométrique de positions, mais plutôt comme organisation mutuelle des fonctions, c’est-à-dire comme comportement réglé.

Il reste à identifier l’analogue du flux d’entropie : en morphodynamique, la transition de phase s’accompagne d’un flux de complexité par déplacement de fonctionnalités vers l’environnement. D’une part, la complexité diminue car le nombre de valeurs des variables est réduit dans le système : il se simplifie en corrélant dans un comportement inédit des fonctions auparavant fluctuant indépendamment les unes des autres. D’autre part, l’environnement se complexifie car il oppose à ce comportement des valeurs de fonctions auparavant inexistantes. Par exemple, une espèce animale peut envahir un territoire si elle a des facultés sensori-motrices suffisantes, c’est-à-dire une température complexe assez élevée. En effet, elle doit d’une part surmonter la sélection naturelle que l’environnement exerce, notamment au travers des ressources qui sont limitées. D’autre part, elle manifeste des comportements inédits à l’égard des espèces résidentes, mais celles-ci étendront la gamme de leurs conduites pour y faire face, telles que agressions plus vives ou fuites plus rapides. Le théorème de croissance de la complexité donne ainsi un résultat inattendu : les conduites induites dans l’environnement dépassent en nombre les fonctions corrélées dans les comportements spécifiques de l’envahisseur. Le dépassement dépend de l’écart des températures complexes, et il constitue le facteur statistique indispensable pour stabiliser la nouvelle espèce dans le milieu.

Ainsi, tout comme la transition de phase en physique, la transition à l’ordre fonctionnel exige que l’environnement remplisse des conditions particulières que le système ne contrôle pas. Mais lorsqu’elles sont présentes, la transition est nécessaire et spontanée ; le processus est non-rationnel dans le sens qu’il ne relève pas de la logique formelle ou d’algorithmes mathématiques. En morphodynamique s’ajoute toutefois une condition spécifique des structures fonctionnelles : le taux de production mesuré par les constantes K des Éq. (5.1) est un cofacteur de stabilité ; en conséquence, une sélection interne s’opère qui favorise les performances les plus élevées (Fivaz 1995).

Inférence 6. Selon la thermodynamique, la transition de phase suscite un paramètre d’ordre dans l’espace dont dépendent les interactions. En morphodynamique, les paramètres d’ordre sont d’abord créés dans l’espace fonctionnel, mais ils interagissent dans l’espace de configuration ; s’ils sont en nombre suffisant, ils peuvent à leur tour créer un paramètre d’ordre spatial qui décrit un arrangement telle que forme ou structure. La raison en est que les interactions entre structures sont assurées par des flux mobiles qui s’étendent dans tout le système : ni le contact ni la distance ne limitent le nombre des structures couplées, et pourtant les interactions restent rapides lorsque les flux sont organisés en circulations comme on le voit souvent dans les organismes réels. Par conséquent, les interactions peuvent être à la fois fortes et de longue portée : ces propriétés conduisent à des paramètres d’ordre variés et très stables, et qui peuvent ensuite se combiner pour établir des régulations raffinées. Dans un système hypercomplexe, cette procédure peut se répéter plusieurs fois. Elle construit alors une hiérarchie à niveaux multiples où les paramètres d’ordre alternent dans l’espace des fonctions et des structures.

Tous les phénomènes répertoriés ci-dessus sont irréversibles et participent à l’évolution spontanée des systèmes complexes vers la prolifération, la diversification et l’organisation : l’évolution spécifie un “temps biologique” doué d’une flèche analogue à la flèche du temps thermodynamique. Cette nouvelle flèche du temps reflète les deux problèmes que la matière vivante a su résoudre pour durer : d’une part, elle affronte des conditions d’existence aléatoires et donc imprévisibles ; d’autre part, le couplage entre ses éléments au niveau microscopique la rend instable au niveau macroscopique. La solution a consisté à exploiter l’instabilité pour faire face à l’imprévisible sur le champ. Cependant, comme on vient de le mentionner, les structures capables de le faire se trouvent assujetties à une sélection visant la performance ; la solution a donc définitivement voué la matière vivante à l’accélération et au perfectionnement des fonctionnalités. A partir de ces considérations, il est raisonnable d’envisager que la vie prenne son essor dès que le mélange adéquat d’agents chimiques existe : avec le temps, l’évolution biologique est toujours plus rapide et rien ne semble limiter ses compétences hormis les problèmes de taille liés à la chimie elle-même.

La morphodynamique suggère ainsi que nous pouvons comprendre le développement de la vie de la même façon que la prévalence de l’ordre dans la matière physique. L’intelligibilité reste toutefois plus faible qu’en physique bien que le nombre de variables par composant soit plus bas : la raison en est que la biochimie autorise des espèces de composants en bien plus grand nombre. En effet, il n’existe pas en biologie l’équivalent des règles de quantification qui limitent le nombre d’espèces en physique (Barrow 1991). Leur absence évidemment multiplie les combinaisons possibles et met notre esprit au défi de trouver un nombre fini de règles couvrant même les plus complexes de ces combinaisons.

Parmi elles se trouve d’abord l’ADN avec son pouvoir unique de conserver le patrimoine génétique sous forme symbolique et de le programmer à chaque reproduction : pour la première fois, une théorie donne la clef de ce pouvoir en démontrant que comportements et messages sont convertibles entre eux. L’évolution se distingue ensuite par le processus d’encéphalisation qui est sans doute l’exemple de complexité croissante le plus frappant. Selon la morphodynamique, ce processus est spontané : il commence à la naissance de la vie et aboutit aux conquêtes technologiques actuelles. Il a ainsi passé par les transitions morphodynamiques instaurant des organisations de plus en plus complexes : construction de cellules contrôlant leurs échanges avec l’extérieur, composition d’organismes d’autonomie croissante, puis naissance de l’intelligence, enfin émergence de la conscience comme fruit plausible de l’interaction sociale par le langage (Jaynes 1976). Certaines théories évolutionnistes ont déjà envisagé de telles successions de transitions (Felden 1994), mais sans en identifier les mécanismes responsables ; la démarche scientifique commande alors de conclure que « rien ne contraint la vie à évoluer » afin de bannir toute prémisse téléologique (Barrow 1991). Or, la morphodynamique propose désormais un mécanisme de transition précis : il comporte certes des aspects non-rationnels mais ils sont justifiés empiriquement par la physique. Comme théorie évolutionniste, elle reconnaît par exemple qu’il existe des processus internes qui tirent le meilleur parti des spécificités des organismes ; elle explique ainsi la genèse du plus apte au cours de l’évolution biologique, alors que les théories darwiniennes ne peuvent que constater passivement la survie du plus apte. Ces processus vont évidemment assurer la survie face aux pressions externes de la sélection naturelle, et cela de façon bien plus efficace que les seules mutations aléatoires invoquées par les théories darwiniennes. La sélection interne peut aussi retenir des originalités même si elles semblent marginales pour la survie, par exemple le cou de la girafe ou le cerveau humain. La morphodynamique rend finalement intelligible le fait avéré que les organismes sont contraints de s’adapter, et que certains en ont acquis à la longue des compétences extrêmement perfectionnées.

7. Temps et interactions au niveau mental

Le perfectionnement trouve son aboutissement dans les systèmes mentaux : ils se distinguent des autres systèmes vivants par la prépondérance des échanges qu’ils entretiennent avec des partenaires de complexité comparable. Ces échanges constituent des interactions d’une classe supérieure puisqu’ils agissent comme des influences répulsives ou attractives sur chacun des partenaires. Les activités correspondantes exigent néanmoins des structures spécialisées reconnaissant facilement (petites valeurs D) les signaux externes I appelant les fonctions expertes dans ces échanges (grandes valeurs K). La présence de ces structures spécialisées requiert de réinterpréter la température complexe définie par l’Éq. (5.2) : pour les systèmes mentaux, cette variable représente le niveau de connaissance sur le contexte socio-culturel, ou l’expertise générale atteinte dans les domaines d’activité. Il en résulte une interprétation avancée de la morphodynamique et dite “cognitiviste” : elle implique que les interactions entre individus produisent des paramètres d’ordre abstraits, supra-individuels et hiérarchisés. En construisant ainsi un ensemble cohérent de normes qui régissent les conduites réciproques, ces interactions nouvelles ouvrent effectivement la voie à l’organisation sociale.

Dans cette interprétation avancée de la morphodynamique, les individus sont considérés comme des systèmes complexes distincts mais couplés par leurs échanges macroscopiques. Comme indiqué par les inférences 1 et 2, ces échanges ont deux modalités consistant en comportements, suites ordonnées d’actions réelles, et en messages, suites non-ordonnées de symboles. L’originalité de la théorie est d’alléguer qu’un système mental a la capacité de transformer ces modalités l’une dans l’autre sous l’égide de principes mathématiques selon l’inférence 3 : par construction même, tout système mental est capable de décrire un comportement par un message, et, inversement, il est capable traduire un message en un comportement. Les messages formalisent donc dans un code symbolique les comportements qui constituent leur sens. Comme l’ordre physique peut être transitoire sous forme de travail mécanique, ou permanent sous forme de structure cristalline, le sens peut être transitoire ou permanent : le premier cas est l’histoire comme narration unique d’événements circonstanciels, le deuxième est la proposition formelle dont on peut vérifier le statut durable de vérité ou d’erreur.

Ces relations inattendues entre la matière physique et la signification ont longtemps figuré parmi les questions les plus mystérieuses que posent la matière vivante et son évolution vers l’activité mentale (Pattee 1995). Maintenant, la morphodynamique montre que ces relations se fondent dans la dynamique macroscopique que les systèmes complexes possèdent comme ensembles de structures fonctionnelles : comportements et messages se transforment précisément comme se transforment travail et chaleur dans les ensembles de particules qui forment les systèmes physiques. Il est vrai que ces transformations ne sont pas directement accessibles à l’intuition, et elles posent encore les problèmes de compréhension qu’affrontaient les thermodynamiciens avant Boltzmann. Effectivement, matière et sens se raccordent par l’intermédiaire de l’hypothèse ergodique qui est non-rationnelle et dépasse le discours logico-mathématique ; pourtant, nous sommes sûrs de nos connaissances de physique, et elles devraient nous persuader de dissiper l’aura de mystère qui entoure l’épistémologie encore aujourd’hui.

Explicitement, la théorie montre comment les structures matérielles deviennent des symboles, et comment ceux-ci en retour commandent la construction des structures. Plus généralement, elle montre comment s’établissent les correspondances entre le concret et l’abstrait, ou encore entre biens matériels et biens immatériels. L’exemple immédiat est l’observation scientifique des phénomènes naturels. C’est le processus par lequel un observateur extrait le comportement d’un objet à partir de ses configurations successives : parce qu’elles suivent les variations incoordonnées de l’environnement réel, les configurations apparentes manifestent un comportement ergodique, et celui-ci aboutit à l’émergence d’un paramètre d’ordre unique entre variables internes selon l’inférence 6. Ainsi, l’observateur découvre le comportement spécifique de l’objet, et il en invente une représentation formalisée dans un langage a priori arbitraire. Ces deux actes mentaux non-rationnels se succèdent pour transformer l’observation en connaissances transmissibles : la morphodynamique aboutit donc à une épistémologie formelle des connaissances scientifiques (Fivaz 1996 a). Pour prendre l’exemple de cet article, l’épistémologie aboutit aux conceptions du temps qui diffèrent pour les systèmes physiques ou vivants ; pour ce faire, elle utilise l’observation de nombreux événements aléatoires dont finalement émerge une série de paramètres d’ordre indépendants de l’observateur. En physique, de tels paramètres sont spécifiques du système et non du contexte ; par conséquent, ils sont auto-déterminés. Par analogie, les systèmes mentaux construisent des paramètres d’ordre qui sont auto-référentiels : au plus haut niveau, ils s’imposent comme des croyances a priori qui fondent notre connaissance de la réalité, et, comme avancé en Sec. 2, ils pourvoient à l’adaptation mentale qui nous rend maître des aléas façonnant cette réalité.

Mieux encore, ils induisent le développement permanent de la société : les inventeurs reprennent les connaissances scientifiques établies et conçoivent des comportements artificiels inédits par transformation inverse. Leurs succès prouvent que les connaissances étaient suffisamment libres de préjugés : l’objectivité apparaît alors comme l’indice de la réversibilité des transformations qui ont créé les connaissances. Comme critère de validation des connaissances, la réversibilité est plus exigeante que l’indépendance des observateurs car elle exclut les cas où les observateurs ont tort même s’ils sont d’accord.

Dans les sociétés modernes, les transformations entre comportements et connaissances sont arbitrées par la monnaie, autre ensemble symbolique qui a la faculté de concilier les disponibilités techniques et les besoins sociaux. Par cet arbitrage, le travail humain et les produits manufacturés acquièrent avec la connaissance et le capital des relations rigoureuses qui étayent une théorie économique universelle (Fivaz 1996 b). Elle révèle non seulement le rôle décisif de la connaissance dans la croissance économique, mais aussi le rôle complémentaire de la monnaie comme information sur l’état du système économique : loin d’être le trivial instrument de pouvoir souvent décrié, la monnaie sert à comptabiliser les réserves que l’humanité a constituées par son travail et qu’elle peut ensuite consacrer à son effort de civilisation.

Finalement, puisque l’humanité est privée de tout message externe et ne suit que les instructions qu’elle se donne elle-même, elle constitue un système faîtier isolé au sens morphodynamique. En conséquence, son savoir et ses activités s’étendent et s’organisent de façon permanente et irréversible, tout en gagnant en complexité selon les inférences 4, 5 et 6. L’évolution socio-culturelle est donc spontanée et irréversible, et elle résulte essentiellement des interactions répulsives et attractives qui s’exercent entre les individus par l’intermédiaire de leurs échanges réels ou symboliques. C’est le rôle de la culture de spécifier la nature de ces interactions : elle stipule par exemple les conventions selon lesquelles les comportements individuels s’excluent ou s’enchaînent. Explicitement, elle désigne ce qui fait, du point de vue social, le sens et le non-sens, le cohérent et le contradictoire, ou le désirable et l’inacceptable (Bruner 1986). La culture crée et perfectionne à cet effet des systèmes symboliques riches et raffinés, tels que les langages et les institutions. Par exemple, elle consigne les meilleurs modèles d’action et d’interprétation dans les manuels et les œuvres d’art, et les écoles les exposent systématiquement. Grâce à ces conventions culturelles, les personnes peuvent donner un sens pertinent à leur expérience privée et identifier les fonctions avantageuses qu’elles peuvent remplir dans la société.

Avec ces divers exemples, le lecteur constatera que la morphodynamique aboutit à une théorie générale des activités humaines et de leur incessant perfectionnement. Elle fonde la civilisation sur l’épanouissement des sciences ; ce terme couvre ici les sciences exactes aussi bien que les sciences humaines, y compris l’épistémologie comme science des sciences. La théorie reconnaît le développement mental ou social comme un processus irréversible qui n’est pas instantané mais qui se déroule dans le temps : comme l’établissement de l’ordre en physique, l’établissement de compétences ou d’idées nouvelles exige du temps. La stabilité de l’ensemble exige même que les durées croissent avec le niveau d’organisation, car les interactions à ce niveau ne doivent pas prendre de vitesse celles qui stabilisent les niveaux inférieurs. La richesse des interactions compense leur ralentissement : par exemple, les échanges entre hommes sont plus diversifiés et mieux propagés que les échanges entre neurones. Ces connexions justifient que les phénomènes qui se déroulent aux plus hauts niveaux hiérarchiques prennent plus de temps ; leur durée caractéristique peut donc servir de critère pour élucider l’emboîtement des niveaux hiérarchiques. Par exemple, l’apprentissage et l’invention au niveau individuel se déroulent dans le temps mental sur des durées de l’ordre de l’année, tandis que le savoir et l’innovation au niveau collectif se déploient dans le temps socio-culturel sur des durées de l’ordre de la génération. Enfin, les civilisations ont elles-mêmes des durées de maturation de l’ordre du siècle, mais ces durées se réduiront sans doute avec les nouveaux moyens de communication.

8. Conclusions

La morphodynamique est une théorie générale de l’évolution qui lie formellement la complexification des êtres vivants au déroulement du temps. La pensée empirique a reconnu le lien depuis longtemps, mais il restait à reformuler le problème épistémologique sous-jacent. Ainsi, la théorie actuelle est en mesure pour la première fois de dégager les hypothèses logiquement nécessaires pour expliquer ce lien entre temps et complexité. La première hypothèse est que le système complexe soit constitué de structures fonctionnelles, c’est-à-dire d’éléments exécutant une fonction liée dynamiquement à leur structure. La deuxième hypothèse est que les structures aient des interactions faites à la fois de compétition et de coalition avec leurs partenaires. La dernière hypothèse est que le système se trouve dans un environnement suffisamment variable pour qu’il explore toutes les configurations possibles de ses éléments. Lorsque ces trois conditions hautement plausibles sont réunies, le système tend spontanément vers un équilibre fonctionnel. La tendance se manifeste dans un temps spécifique des interactions, et elle consiste non seulement en expansion où la compétition joue le rôle moteur, mais aussi en organisation qui au contraire repose sur la coalition entre composants. Enfin, la tendance confère aux systèmes complexes la capacité de manipuler les symboles : ils peuvent ainsi sauvegarder et reproduire les comportements qui assurent la pérennité face à l’imprévisible.

Ainsi, la théorie explique que certains systèmes vivants atteignent dans leur temps propre des degrés de compétence arbitrairement élevés, et cette explication va bien plus loin que les théories darwiniennes de l’évolution. En premier lieu, l’explication est rationnelle précisément au même titre que l’explication thermodynamique l’est pour l’ordre dans la matière. En deuxième lieu, l’explication fait état d’une sélection interne originale : elle favorise la performance avec un discernement dont la sélection naturelle ne dispose pas. Enfin, l’écoulement du temps prend sa pleine signification dans le rôle qu’il joue pour édifier des structures vivantes ou sociales jusqu’aux plus hauts niveaux d’organisation. D’un point de vue philosophique, l’apport majeur de la morphodynamique reste la démonstration rigoureuse d’un principe de croissance dont on soupçonne depuis longtemps l’existence pour la vie et l’intelligence (Felden 1994). Ce principe s’applique aussi à l’organisation socio-économique : en accord avec la pensée libérale moderne, il indique que la concurrence brute est certes le moteur de l’expansion quantitative, mais il rappelle avec éclat que les acteurs sont tenus de collaborer s’ils veulent ménager les aspects qualitatifs de la civilisation.