Les informations sur la culture du XVI^e siècle européen que porte le livre mathématique

Jean DHOMBRES

Centre Koyré, EHESS, Paris

En introduction j’aurais voulu présenter un bilan de travaux sur le livre mathématique, permettant d’apprécier la ligne générale des questions traitées, pour éventuellement suggérer de l’infléchir en tenant notamment compte de productions récentes. Mais je dois reconnaître qu’il n’existe pas de littérature conséquente sur ce thème¹, en tout cas pas au niveau du nombre considérable d’études sur les mathématiques de la Renaissance. C’est ainsi qu’il n’y a aucun article à ce propos dans le premier volume sorti en 1982 de l’Histoire de l’édition française sous la direction de Henri-Jean Martin et Roger Chartier². Pourtant, en l’absence de journaux savants et en l’absence de congrès de mathématiciens au XVI^e siècle, l’information mathématique ne circula que par le livre, dont la forme justement eut à se trouver, et plus encore lorsqu’il fallut façonner un nouveau lectorat en dehors de celui relativement captif des universités. Celles-ci dispensaient un enseignement formaté par les seules sciences mathématiques du quadrivium, qui n’incluaient ni algèbre, ni arithmétique commerciale, mais pouvaient quand même servir à la navigation par la représentation de la sphère.

Les recherches portèrent essentiellement sur l’épistémologie, car on voulait tenir compte du phénomène qu’était la lenteur d’innovation mathématique aux XVI^e et dans la première partie du XVII^e siècle, en comparaison de ce qui allait se passer avec la révolution scientifique : celle-ci culminera avec le Calcul différentiel et intégral indispensable à la compréhension de la nouvelle vision du monde instaurée par Isaac Newton avec les Principia mathematica philosophiae universalis de 1687. Cette vision différentielle servit de support et même de moteur pour les mathématiques des Lumières en oblitérant largement les procédures mathématiques antérieures. Si parfois on voulait cependant indiquer par le livre une première « révolution » à la Renaissance, c’était pour le passage de l’édition des mathématiciens grecs retrouvés à un exposé critique de ces mêmes auteurs, et enfin à leur abandon. C’était en particulier reconnaître que la disposition du livre n‘était pas un enjeu.

On s’intéressa bien plus à la fidélité à l’original antique, souvent supposé unique, incontesté et de forme invariable, jusqu’au reniement sous l’effet de pensées nouvelles, précisément dites modernes et survenues à une époque qui ne concerne pas le présent recueil. Pour l’analyse de ce premier changement, les érudits négligèrent donc les aspects liés à la présentation matérielle du livre³, comme le jeu des figures qui ne pouvaient plus être des schèmes à la va-vite et à la main ; elles requéraient en effet un artisan intermédiaire, le graveur (qu’il soit sur bois ou sur cuivre), et ainsi une économie du travail dont par ailleurs les historiens du livre surent remarquablement dire les linéaments. Je n’ai pourtant pas lu de pages consacrées à cette liaison particulière pour le livre mathématique, et je serai donc bien en mal pour en tirer des conclusions. Aujourd’hui pourtant, c’est peut-être dans l’intérêt porté à l’image que l’histoire du livre trouve son élan le plus net – ce qui, en mathématiques et pour le livre, devrait accompagner le souci de ce que l’on appelle maintenant des diagrammes, abandonnant aussi bien le vocabulaire des images que celui des symboles. N’installe-t-on pas cette distinction sémantique utile pour sortir du préjugé sur l’illustration comme distraction, embellissement, voire appel au rêve ?

Ma première réflexion doit porter sur les raisons qui peuvent expliquer le peu d’études sur le livre mathématique, avant d’en venir aux informations que l’on peut effectivement tirer de l’étude de quelques séries de tels livres. La première raison d’un dédain tient à la forme de l’écriture mathématique, quand elle est dogmatiquement présentée comme un code incompréhensible aux non initiés et en fait comme une symbolique. Elle serait dès lors en opposition avec le sens transparent des figures dont la plupart des livres mathématiques sont remplis. Cette contradiction a priori constitue le handicap majeur.

LA QUESTION DU CODAGE DES TEXTES MATHÉMATIQUES

Jusqu’à présent en effet, quasiment les seules illustrations dites mathématiques envisagées dans les études sur le livre illustré concernent la perspective ⁴, car il est pensé que cette perspective est ce qui fait « passer » l’abstraction des figures géométriques : voir l’illustration 12, datant de 1572, comme explication des illustrations bien antérieures 10 (1482) et 11 (1533). Or la perspective est une science dont le lien avec les mathématiques au XVI^e siècle touche la seule question de la représentation de l’espace sur la feuille plane, et non la structure des figures géométriques les plus usuelles, qui sont planes. Certes elle montre la validité des ellipses de l’illustration 12, qui débordent un peu sur ce qui du coup n’est plus un contour apparent, et leur avantage visuel par rapport aux courbes anguleuses de l’illustration 10 et au fouillis de l’illustration 11. Toutes ces figures n’en servent pas moins à la même démonstration de la même proposition du livre XII des Éléments d’Euclide, et grosso modo selon les mêmes modalités. Quelle est l’utilité réelle de la figure soignée quand il s’agit d’inscrire un polyèdre dans une sphère, de telle sorte que le polyèdre ne rencontre pas une autre sphère intérieure ? C’est un simple confort, et peut-être dans le livre une marque de la professionnalisation du graveur.

Si ce sont ces formes, perspectivistes ou non, qui font qu’est d’emblée diagnostiqué un livre de type mathématique, on doit reconnaître justement à la Renaissance le surgissement d’une autre forme qu’est l’écriture de l’algèbre. Elle est trop vite dite symbolique, voire signe et donc absence de volume, alors qu’elle occupe tout aussi bien un espace de la feuille plane imprimée. Cet espace est bien différent de l’espace structuré par les alignements des lignes d’un texte. Il y a en effet un jeu du haut et du bas, des exposants, des colonnes, ou des accolades, et surgissent aussi bien ce qu’on appelle des tables ou tableaux, dont le nom seul évoque matériellement l’espace (ill. 2, 3 et 4). Tirée d’un ouvrage de Viète en 1591, l’illustration 2 est révélatrice de cet effet, puisque l’on voit en marge et noté à la main un difficile essai de plus grande spatialisation par l’emploi de lignes horizontales, nos barres de fraction : dans les dernières lignes de Viète il est expliqué en langue algébrique sans formule, mais pas sans écriture littérale ou spécieuse, comment mettre sous forme d’une seule fraction la différence de deux autres⁵. Se présente donc la règle élémentaire du dénominateur commun, dénominateur en l’occurrence noté par Viète B in G comme on le repère sur l’original selon une écriture syncopée pour désigner le produit de B par G. Peut-être préférera-t-on parler d’un geste de calcul, mais pour le cadre du livre que j’ai choisi, cette gestuelle est seulement manifestée par une spatialisation, qui la rend usuelle, sinon banale. Et l’air de rien s’introduit une nouvelle opération de type numérique, une soustraction, sur les raisons dans les proportions auparavant seulement soumises depuis le livre V à la multiplication.

Si donc je peux utiliser l’affirmation générale de Michel Pastoureau selon lequel l’image codée ne peut avoir de succès durable dans le livre imprimé⁶, je le fais pour expliquer l’absence d’intérêt des historiens pour les formes graphiques évolutives et banalisantes du livre mathématique. Certaines de ces formes ont de fait émigré du livre mathématique vers le sens commun, ou aussi bien se sont installées dans le livre sous la pression de ce même sens commun éduqué par la mode. Que le livre mathématique soit caractérisé par des codes spécifiques ne revient pas à dire que tous ces codes n’ont rien de naturel pour la plupart des lecteurs. La perspective est une représentation devenue naturelle (ill. 4), mais je crois que l’organisation de tableaux numériques est tout autant devenue familière (ill. 3), comme la pratique fractionnaire pour les raisons. Par contre, les formules de l’algèbre ne le sont toujours pas, et une expression qui va survenir partout au XVII^e siècle reste mystérieuse (sauf bien sûr à tous les lycéens d’aujourd’hui, mais c’est une autre histoire qui tient à la mentalité française adulte, et à la peur rétrospective pour tout ce qui est scolaire ou technique).

En écrivant le mot de représentation, j’ai risqué de faire oublier que la perspective était d’abord un code du voir de l’espace, dont la naturalité est provenue d’une construction historique de la sensibilité, apprivoisant les plus anciennes formes des figurations géométriques. Si peu reconnaissent cette naturalisation comme issue du livre mathématique, je ne vais pas entrer dans un vain débat sur la primauté du théoricien ou de l’artiste, lorsque précisément l’artiste était aussi bien mathématicien, en tout cas aussi savant qu’un mathématicien. Mais le XVI^e siècle connaît une autre révolution du comprendre que la perspective. Sur le fond abstrait, le changement était reconnu depuis longtemps des historiens mathématiciens, et il suffit d’exhiber le titre choisi par Rafael Bombelli en 1572, puisqu’il s’agit de l’Algèbre. Les choses se compliquent dès lors que l’on fait lire le titre Nouvelle algèbre, choisi par François Viète en 1591, ou Art analytique, avec l’apparent paradoxe qu’il s’agirait d’une restitution d’une méthode antique. Y aurait-il à tout le moins des algèbres si différentes dans un si court laps de temps ! La nouveauté européenne de l’algèbre entraînerait-elle un sentiment de nouveauté perpétuelle ? Qui signerait la modernité baroque, comme étant une constante remise en cause, et aboutirait forcément à la Querelle des Anciens et des Modernes ? Sauf à prétendre que cette modernité serait enfin une bonne interprétation de l’inventivité antique, sautant d’ailleurs par dessus l’héritage arabe. Je ne tranche pas plus en l’occurrence, mais me contente de noter que c’est dans un livre où il y a la banalisation des fractions que l’on trouve la preuve que Viète entendait poursuivre un programme algébrique complet (ill. 1). Il le donne à lire en 1591, et il prend d’autant plus la liberté de le faire qu’il doit travailler à compte d’auteur. Il n’y a aucune chance que son travail franchisse alors les portes de l’université. Et quand la chose sera possible, il sera trop tard, car cette algèbre des formes homogènes sera obsolète, remplacée par l’algèbre des formes polynomiales.

Les listes qui furent effectivement données des livres d’algèbre⁷ ne cherchent pourtant pas à établir un quelconque hiatus, sauf peut-être récemment dans le cas d’une algèbre nationale « anglaise »⁸, mais elles correspondent à l’idée qui se fait jour de traditions nationales différentes, en Italie ou en France. L’algèbre, première ou deuxième forme, mais aussi et surtout l’origine de l’algèbre dans le monde arabe, sont présentées alors de façon continuiste comme une même discipline qui se forgerait peu à peu, chargée plus tard d’être un des prolégomènes indispensables pour l’apprentissage du calcul différentiel et intégral, dont elle serait aussi le signe avant-coureur. On ne souligne donc pas assez que le parti pris axiomatique de Français Viète en 1591 lui fit adopter un style quasiment euclidien. Qu’il soit aussitôt dit « géométrique », alors même qu’il n’y a pas beaucoup de figures, fait courir le risque que le sens commun associe cette « géométrie » à celle des tracés. Le parti pris historique sur l’algèbre de l’Anglais Wallis, soixante années plus tard, consistera à manifester l’abstrait dans le maniement des symboles, en faisant intervenir l’induction portant sur les formes algébriques et non sur les formes géométriques. Ce raisonnement, qui était bien différent de la méthode axiomatique, pouvait avoir déjà été rencontré dans les arithmétiques anciennes, et leurs tables numériques, et aussi bien dans les calculs trigonométriques avant la lettre, en astronomie, en navigation et encore en géodésie.

Justement, il y a quelque avantage à présenter les tables numériques à l’aube de la société du quantitatif, avec les modes d’emploi réunis en latin sous le nom de canones (ill. 3), comme des diagrammes installés dans l’espace de la page. Les tables, faut-il reconnaître, entrèrent tardivement dans le champ critique des historiens des sciences eux-mêmes⁹. Si cet intérêt bien nouveau manifeste la spécialisation technique qui s’affirme dans de telles études, il n’en correspond pas moins à une bonne adéquation avec la description générale et déjà ancienne de cette période où la quantification sous la forme des échanges bancaires prit une grande place. C’est la publication des tables d’intérêt bancaire qui lance en 1582 dans le livre un mathématicien aussi remarquable que Simon Stevin¹⁰. Or si on s’est enfin convaincu, sur l’exemple fétiche des tables de logarithmes à partir de 1614, que l’abstraction du numérique tabulé a précédé le graphisme dit naturel des courbes qui est notre usus de perception aujourd’hui¹¹, ne risque-t-on pas en réaction d’attribuer un caractère purement analytique aux tableaux numériques ? On en oublie leur spatialisation qui les rend faciles à lire, que ces tableaux se trouvent dans des documents comptables, dans des relevés d’astronomie ou encore dans des chartes nautiques. Je me garde de les confondre avec les cartes géographiques qu’il n’est pas raisonnable de ranger dans la liste des livres proprement mathématiques, quand bien même les contemporains appelaient « mathématiciens » leurs fabricants.

Ne peut-on aussi traiter ces tableaux numériques à la manière des formules de l’algèbre, cette activité qui précisément en Europe faisait une entrée remarquable dans le champ savant, à partir du monde marchand ? Mais bien rares sont ceux qui reconnaissent à ces formules une valeur spatiale à la manière dont on le fait pour les figures et les images. Je dois d’abord préciser sur un autre exemple mes remarques sur le caractère premier des tables logarithmiques en avant-coureur de la courbe. Car dans le cas des loxodromies, ces routes de la mer qui correspondent à des tracés sur la sphère terrestre à angle constant avec les méridiens, un dessin esthétique ou plutôt rêvé à partir de portulans du Portugais Nunes cohabite avec un dessin d’approximation et encore avec une table numérique qui semble expérimentale. Edward Wright en 1599, dans les Certaine Errors in Navigation, detected and corrected…, donne une table calculée par somme approchée de sécantes, que l’on interpréta à la fin du XVII^e siècle comme le logarithme d’une tangente d’arc moitié du complément à un droit de la latitude¹². Or, cette fonction même justifie précisément les écartements vers le Nord des degrés de longitude sur la carte de Mercator, et c’est enfin la courbe en projection stéréographique d’une loxodromie, une spirale logarithmique, qui synthétisera toute la théorie moyennant le caractère conservateur des angles de ladite projection, réunissant au final, mais seulement vers 1696, calculs, courbes géométriques et cartographie¹³. Edmund Halley parlera alors d’une analogie prouvée.

Des images stricto sensu de perspective, mais les formes aussi de l’écriture symbolique, ont fait l’objet des deux seules interventions récentes sur le livre mathématique, l’une de Laurent Pinon et l’autre spécifiquement algébrique d’Aude Le Dividich, dans Mise en page et mise en texte du livre français : la naissance du livre moderne, dirigé par Henri-Jean Martin en 2000¹⁴. Il manque cependant l’étude des relevés numériques, que je crois nécessaire d’associer. La sage histoire du livre réclamant des séries, et j’ai choisi plus loin deux séries déjà assez bien étudiées, d’une part les livres des Mechanica et d’autre part les éditions des Éléments d’Euclide, je dois néanmoins reconnaître le manque de travaux sur les tables numériques, alors même qu’elles sont passées dans le banal du voir comme du comprendre. Au moins, par le passage à la spatialisation, j’ai pu indiquer pourquoi certaines présentations du livre mathématique sont devenues naturelles et sans symbolisation incompréhensible.

À ce stade, il me faut parler des frontispices de livres mathématiques, car si leur jeu très codé est manifeste, je veux montrer qu’il est quelquefois peu déchiffrable, c’est-à-dire ambigu, et que ce dernier effet est voulu, même pour un livre de science qui vise à l’exactitude. Mon projet est bien de débarrasser les sciences mathématiques s’exprimant par le livre de la préconception qu’elles n’auraient formellement rien à dire sur une époque que du trivial ou de l’ésotérique. L’établissement du banal, comme celui copernicien qu’on peut lire aujourd’hui dans le frontispice de l’édition Riccioli de 1651, et qui passe par le spatial plan des oppositions de l’ombre et de la lumière comme je vais le montrer (ill. 5), est facilité par le passage par une mise en doute qui fait ésotérique. N’est-ce pas d’abord ce qui a été lu sur l’exemple manuscrit expliquant la réduction de fractions algébriques à un même dénominateur commun ? Et c’est bien l’histoire du livre, par les notes marginales, qui l’atteste.

FONCTIONS CODÉES DU FRONTISPICE

Dans les études portant sur l’illustration du livre de mathématique, et d’ailleurs sur le livre de science en général, un autre des présupposés, les plus usuels malheureusement, est d’envisager l’art comme un moyen qui, parce qu’approximatif, serait a priori inférieur à la matière traitée. Un érudit parfait au tournant des XIX^e et XX^e siècles, Henri Bosmans, spécialiste de la science à l’âge classique, se voulait dépréciateur en parlant de « vignettes gracieuses » à la mode de Rubens à propos d’une thèse illustrée de 1624 portant sur la mécanique, alors que ces vignettes signalent explicitement la loi toute nouvelle de la chute des corps de Galilée, et la font voir par la manière imagée qui correspond à la mode baroque. Le dessinateur et graveur participe de la vie scientifique, sans pour autant utiliser la formulation algébrique que peut-être il ne maîtrise pas¹⁵. Mais cela n’a pas été reconnu, car en science l’art a souvent été pensé comme un moyen rhétorique au sens vulgaire du terme, donc faux, ou à tout le moins prêtant à une confusion dont la science prétend toujours se débarrasser. Ce ne pouvait être le système de pensée à l’âge baroque, même si l’on peut envisager le passage à l’âge classique comme manifestant la mise en œuvre d’une telle dépréciation. Elle n’a cependant lieu qu’une fois la science assurée de la réalité de son abstraction. C’est encore en gros le jugement de type positiviste, puisque Comte dénigrait à l’art le pouvoir de dire le vrai, et tout particulièrement le vrai qui soit utile à l’homme ; il préférait de très loin l’ingénieur à l’artiste, le mathématicien Monge de la géométrie descriptive à l’abbé Delille versifiant en français les Géorgiques, et dénigrait la façon du médecin idéologue Alibert s’aidant d’un peintre pour décrire les maladies de la peau.

Dit autrement, dans les termes du débat déjà ancien sur la sociologie des sciences, l’art est pensé comme extérieur à la science : au point que la constitution d’un corpus d’images n’est venu que tard de la part des historiens des sciences proprement dits, et bien peu d’entre eux aujourd’hui signalent que le Dictionary of ScientificBiography comprend depuis 1980 deux volumes intitulés : Album of Science. Je ne les ai pratiquement jamais lus en bibliographie, et je devine que l’une des raisons principales de cet évitement est de compétence : les deux volumes n’ont en effet requis aucun savoir historien de l’art et traitent une image comme si elle avait un sens univoque, quoique toujours bien inférieur au sens de science. Ainsi en fut-il du traitement du frontispice (ill. 5) de l’Almagestum novum astronomiam veterem novamque complectens observationibus aliorum de Giovanni Battista Riccioli de 1651¹⁶ : le commentaire par Charles Coulson Gillispie au deuxième volume de l’Album of Science porte sur le biais du jésuite Riccioli qui, « pesant » le système planétaire de Copernic contre celui de Tycho Brahe, l’héliocentrisme contre un géocentrisme aménagé, ferait pencher la balance en faveur du dernier. Ne faudrait-il pas en dire autant alors de tant de représentations d’un levier équilibré vu en perspective, et par exemple d’une page de titre d’un livre de Jan Pieterszoon Dou en 1620 sur les instruments mathématiques (ill. 6)¹⁷ ? Aucune remarque n’est faite sur l’auteur même de la gravure, comme si cela n’avait aucune importance pour les thèmes iconographiques utilisés. Plus grave encore est l’absence de commentaire sur le fait même de devoir « peser » des systèmes cosmologiques distincts, donc critiquer au « moyen » symbolique d’un instrument la balance, ou levier. Il est par excellence, depuis Archimède, le symbole iconographique de la puissance du raisonnement mathématique, car il matérialise la théorie euclidienne des proportions. Que ce symbole matériel remplace le compas, ou du moins précise pour les grandeurs la fonction d’exactitude de ce dernier s’exerçant sur les figures, peut être lié à la physicalisation des mathématiques que prônait Galilée, entendue comme un réalisme. Symbole bien distinct mais qui va faire pendant, sinon opposition possible, à la lunette astronomique qui, indéniablement, joue l’expérimentation alors même que sa théorie est largement mathématique. En plus, dans le frontispice dû à Curti pour le livre de Riccioli, la balance est une allusion parfaitement lisible par tous à cette époque au livre très polémique de Galilée de 1623, Il Saggiatore : « l’Essayeur », celui qui pèse avec minutie les métaux précieux et jauge par métaphore les arguments sur la comète, en est le thème. Plus symboliquement quoique bien matériellement encore, la disposition des zones de nuit ou de lumière sur les planètes dans ce frontispice, qui dépend bien sûr de leur giration directe autour du Soleil ou de la Terre, peut interroger le dogme du géocentrisme, par l’obscurité qu’elle affiche, sinon son obscurantisme. Ce dogme a été pourtant sanctionné officiellement par la condamnation de Galilée de 1633, et Riccioli est un jésuite obéissant. Dans la description scientiste du frontispice qui est donnée en dernier après une longue tradition dans l’Album of Science furent donc manqués, et son rôle épistémologique et sa fonction dubitative.

Voyons autrement cette fonction au moyen d’une analyse des thèmes littéraires de l’image. Uranie, ou l’Astronomie, la personnification féminine dans le frontispice de l’ouvrage de Riccioli, n’a pas un, mais deux répondants masculins. Le plus attendu, celui de presque toutes les représentations antérieures de l’Astronomie, est Claude Ptolémée. Le voilà presque couché à terre, et son système a littéralement roulé au bas droit du frontispice ! Dans un beau mouvement baroque, le savant antique prétend pouvoir être relevé : Dressé car redressé, ou érigé car corrigé, pourrait traduire le Erigordumcorrigor inscrit dans une bulle. Ce qui veut certes symboliser la possible solution mixte de Tycho Brahé pour les planètes, mais peut aussi signaler l’inquiétante transformation d’une théorie de science en dogme religieux ! L’autre personnage couvert des yeux d’Argus, et dont la face est christique, tient une lunette astronomique. C’est celle qui a permis à Galilée, et tant d’autres à sa suite, de voir autrement les cieux, en particulier d’observer le déroulement des phases de Vénus qui contredit une rotation de cet astre autour de la Terre. S’adressant à Dieu dont on voit la main sortir des nuages et trois doigts pointés – Nombre, Mesure et Poids selon l’expression de la Sagesse (11, 21), ce personnage déclare en reprenant le psalmiste : Videbo caelos tuos, opera digitor[um] tuor[um] ¹⁸ : « Quand je contemple les cieux, ouvrage de tes mains ». La lunette remplace donc le compas que devrait tenir classiquement Uranie. Ce changement iconographique est notable : qu’est-ce qui donne désormais aux mathématiques leur certitude ? Cette question, qu’il faut garder comme une question, fait tout le sens de l’image de ce frontispice. Je n’ai pas eu besoin de considérer l’esthétique de cette image, baroque au point d’en être déséquilibrée, mais tellement caractéristique de l’art jésuite, jusque dans les ribambelles de putti dégringolant sur la droite comme sur la gauche. Ce sont de fait les alternances d’obscurité et de lumière qui marquent le plus le spectateur de ce splendide frontispice dont la composition par un artiste pour le seul livre – il n’y a pas de peinture indépendante – manifeste moins une position qu’une épistémologie de la question. Je n’ai en effet pas besoin de m’interroger sur le lien entre le frontispice et le contenu du livre : les trois systèmes en cause (celui ancien de Ptolémée se trouve en bas) sont explicites¹⁹. Il faut enfin revenir sur la référence mathématique de cette image. On admettra qu’elle n’est peut-être plus dans la représentation des trois systèmes planétaires distincts, car un jeu de cercles était l’habitude astronomique, jusques et y compris pour les épicyles, même si ici il y a un certain réalisme. Il me semble que la balance seule est concernée.

Le sens dubitatif de l’image est peut-être moins apparent dans le frontispice du Saggiatore de Galilée de 1623, auquel la balance de Riccioli renvoie (ill. 5)²⁰. Pourtant, il y a là une première par l’image, avec la confrontation de deux personnifications. Elles sont dûment nommées car on risquerait sinon de n’en reconnaître aucune : il y a la Mathématique, certes couronnée, ce qui n’était pas usuel auparavant, et ainsi pensée comme une par cette majesté régnante. Elle regarde avec assurance à hauteur d’homme, l’index pointé est celui du magister qui désigne la vérité. En face, la Philosophie naturelle, certes rayonnante mais comme modeste, ou peut-être absorbée par une contemplation intérieure, en tout cas différente des diverses personnifications antérieures de la philosophie. Comment ne pas remarquer que les deux personnifications ne relèvent pas du registre des sept arts libéraux (la mathématique n’étant jamais représentée auparavant comme résumant le quadrivium), et que, peut-être conséquemment, elles ne sont plus accompagnées d’une puissance masculine tutélaire, Euclide, Archimède, Ptolémée, Boèce, etc. C’est précisément cette nouveauté iconographique qui me fait dire qu’il y a doute sur la complémentarité des deux personnifications, alors qu’auparavant il y avait équilibre entre l’arithmétique et la géométrie, les deux sciences « abstraites » ou théoriques du quadrivium, auxquelles s’ajoutaient les deux sciences concrètes, ou plus réelles. C’est dans ce texte de Galilée que se trouve la fameuse déclaration : la philosophie est écrite en langue mathématique.

La philosophie est écrite dans ce livre immense qui se tient perpétuellement ouvert devant nos yeux : je veux dire l’Univers. Mais on ne le peut comprendre sans s’appliquer d’abord à en comprendre la langue et à en connaître les caractères avec lesquels il est écrit. Il est écrit en langue mathématique, dont les caractères sont des triangles, des cercles, et d’autres figures géométriques. Sans ces intermédiaires, il est humainement impossible d’en comprendre une parole ; sans ceux-ci, on tourne vainement en rond dans un labyrinthe obscur²¹.

Depuis quelques décennies, ce jugement a été détourné par bien des tenants d’une sociologie constituée de la science, sous la forme d’une explication de la rhétorique mise en œuvre par les scientifiques afin de faire valoir leurs travaux. L’illustration d’un livre, par exemple sous la forme d’un frontispice, serait à l’instar de l’écrin d’un bijou ou d’une parure un moyen de donner du prestige à l’œuvre proprement mathématique, quasiment indépendamment de celle-ci, voire en contradiction avec le sens de cette œuvre. Et dans cette glorification, on néglige ce que la démonstration mathématique porte comme sens. Ainsi l’analyse un des bons livres consacrés aux frontispices anciens²², ajoutant qu’il fallait faire cette réhabilitation des mathématiques.

L’enjeu rhétorique d’une œuvre scientifique appartient évidemment à l’histoire même du livre, puisque le passage à l’imprimé donne une valeur. La leçon s’appliquant à la posture de science a par ailleurs déjà été donnée par Marc Fumaroli dans Ego scriptor, article consacré à la rhétorique de Descartes, ou l’art de ne pas paraître avoir de rhétorique²³. Mais en ne parlant que de glorification et de tentations d’excellence à l’égal de la philosophie, ne détourne-t-on pas le sens de l’image ? Doublement d’ailleurs, puisque d’une part on évacue toute possibilité que l’image marque un doute, comme on l’a pourtant vu avec le frontispice de Riccioli, et d’autre part on fait de la philosophie un idéal qui peut-être était remis en question, si l’on en juge par les aristotélismes et leurs avatars. Fallait-il donner du prestige aux mathématiques, ou en retirer à la philosophie ? Mais voilà que des livres de philosophie ont des frontispices aussi ornés que certains ouvrages mathématiques, d’autres, comme bien des livres mathématiques, n’ayant en revanche aucune ornementation. Après les analyses faites pour les formules, la perspective ou les tableaux numériques, je suis bien plus sensible au jeu de l’espace dans les frontispices, un jeu dans lequel Rubens excella – mais il ne décora pas de livres au XVI^e siècle²⁴.

Me gêne enfin un mélange des genres intellectuels dans la combinaison de ces explications. D’une part, il est envisagé que le besoin de prestige tienne aux mathématiques qui se veulent au plus haut de l’échelle intellectuelle et au plus près de la vérité : une situation qui n’est certainement pas celle des mathématiques du XVII^e siècle. Mais il est aussi envisagé que ce besoin se manifeste par des moyens finalement assez bas, ou jugés tels. Même si l’on fait jouer le fait que les travaux mathématiques sont trop abscons pour que le public général puisse en juger correctement, pourquoi vouloir les orner d’une fausse parure ? Au fond, il s’agit d’agir sur deux fronts contradictoires : avec l’un il serait question du développement interne de la science, avec l’autre de son influence sur un développement externe. La conséquence du développement externe serait une question de marché. Ma gêne tient encore à un anachronisme, celui de considérer que la mathématique, ou la science, a toujours vécu le même régime dans toutes les sociétés, et par conséquent aurait toujours disposé des mêmes armes pour compenser son manque de transparence publique, et que ce manque même serait toujours de même nature. Au moins les deux cas de séries de livres que je mentionne maintenant montrent bien que même sous l’apparence d’homogénéité d’un titre se cachent bien des dissemblances.

UN CAS BIEN TRAVAILLÉ : LES ÉDITIONS DES ÉLÉMENTS D’EUCLIDE, DE LA PREMIÈRE IMPRESSION EN LATIN PAR RATDOLT (1482) À LA DERNIÈRE ÉDITION EN LATIN DE CLAVIUS (1611)

L’édition des Éléments d’Euclide en latin par Ratdolt en 1482 est généralement considérée comme le lancement d’une série qui ira s’agrandissant sans cesse pendant quelques siècles, puisque le livre en question servait en principe à l’enseignement universitaire du quadrivium et que l’on a pu avancer qu’après la Bible il fut le plus édité jusqu’à la fin du XIX^e siècle²⁵. Pourtant le titre de Ratdolt ne peut pas être considéré comme un livre de lecture facile, tant les ligatures et la densité du texte le rendent touffu, et, s’il suit la version manuscrite latine de Campanus de Novara, elle-même issue par Adélard de Bath d’une version arabe²⁶, rien n’indique une utilisation universitaire. D’ailleurs, l’historiographie bien établie des impressions de ces Éléments fait constat d’une concurrence entre deux lectures latines, celle donc directement issue de Campanus de Novara imprimée la première, et celle de Bartolomeo Zamberti, imprimée en 1505 à Venise, qui est issue d’une version grecque corrigée dès l’antiquité par Théon d’Alexandrie²⁷. Aux mirislarvis, ces fantômes imaginés que Zamberti voit chez Campanus, un tenant de ce dernier auteur, Luca Pacioli, réplique en 1509 par la simple correction des fautes de copistes sur le texte « si fidèle » de Campanus de quelques siècles plus tôt²⁸. Une manière de résolution est faite avec la juxtaposition à Paris en 1516, théorème après théorème, des deux textes latins²⁹. La conclusion pour l’histoire culturelle ne peut donc être que l’inscription de ces traductions des Éléments dans le mouvement proprement humaniste de mise en lumière des œuvres antiques, et non dans la démarche de mise à disposition d’un texte pour les étudiants en mathématiques. Cette synopse est d’ailleurs dès son titre dédié aux savants (utcunque noster ualuit labor conciliata sunt haec omnia ad studiosorum non paruam). Il est peu vraisemblable que l’editio princeps du texte grec à Bâle en 1533 par Simon Grynaeus soit sorti de ce contexte d’érudition³⁰.

D’un tout autre genre est la publication des Éléments en 1536 à Paris par Oronce Finé³¹ : il donne les énoncés en grec, mais les démonstrations sont en latin ; cette version suit Zamberti pour la lecture mais la position de professeur royal, en marge donc de l’université, conduit Finé à adapter son texte en vue d’une lecture moderne et d’un usage par des étudiants, ou au moins par des professeurs désirant modifier leur enseignement traditionnel du quadriuium. Il resterait à connaître l’utilisation effective du livre, ou plutôt à reconnaître dans des cours dictés qui nous restent ce qui revient à Finé. Je ne pense pas qu’un tel travail ait été entrepris. Le constat d’un propos éducatif se fait en parcourant la Protomathesis du même Finé, dont précisément le titre signifie une élémentarisation, dont on voit mal où elle conduit³² sinon vers les « mathématiques mixtes » : d’ailleurs Finé trouve l’occasion de placer sa célèbre carte de France. Ces mathématiques mises au service d’autres domaines ne relèvent pourtant pas de la série que je considère qu’en tant qu’extension possible. C’est bien un élève de Finé, Pierre Forcadel, lui-même lecteur royal, qui publie la première version en français, d’abord en 1564, des six premiers livres d’Euclide, puis des neuf premiers livres quelques années plus tard, sans qu’il arrive au dixième, dont en 1585 Stevin déclare en gros l’inutilité³³. La régularité toutefois des éditions de Forcadel, sur une période courte³⁴, peut indiquer un usage universitaire, voire scolaire, encore qu’on n’ait trace d’écoles de mathématiques à proprement parler qu’à partir de 1600 aux Pays-Bas avec Stevin.

La même année 1564, la parution en latin des Euclidae demonstrationes in syllogismos resolutae par Conrad Dasypodius (Conrad Rauchfluss 1532-1600) peut marquer un véritable tournant dans l’édition des Éléments : d’une part le style d’Euclide est modifié pour le rendre compatible avec l’Organon d’Aristote qui fait la loi de la pensée scientifique universitaire et, d’autre part, cet exposé concerne les deux premiers livres seulement – dans les autres livres des Éléments, seules les énonciations sont fournies. La réduction à des énoncés est aussi bien le fait de Pierre de la Ramée, qui en latin en 1549 daigne y ajouter les figures. Mais dans d’autres éditions, les figures ont disparu. En 1624, Mersenne ne donnera pas plus les figures, et évitera toutes les démonstrations dans une Synopsis de textes mathématiques qu’il augmentera (en nombre de textes, mais non pas en démonstrations) en 1644. Même si on se rend compte à quel point les énoncés d’Euclide ne requièrent pas la figure, ces livres sans démonstrations restent une énigme culturelle, et en tout cas questionnent l’idée d’un net mouvement d’acculturation de la démonstration mathématique, qui aurait pu préparer les voies de la révolution scientifique. Mersenne vit hors université, ne l’oublions pas, et préfigure un tout autre mouvement, celui des académies des sciences dans le dernier tiers du XVII^e siècle.

Plutôt que de l’opposer à la version commentée et philologiquement rigoureuse de Commandino, comme le voudrait une analyse usuelle, j’insérerai dans un autre cadre la célèbre série des éditions commentées d’Euclide par Clavius, qui débute en 1574 et ne se termine qu’en 1611. En effet, le professeur de mathématiques par excellence du Collège romain, non seulement modifie Euclide par petites touches, mais par son avalanche de commentaires, notamment sur les proportions rationnelles, sur la logique etc., en fait un guide de logique pratique et une marque pour un enseignement de qualité pour former l’esprit à la pratique réflexive. De façon notable pour mon propos, il insère un tableau de type algébrique dans son commentaire du livre V, par excellence abstrait (ill. 13). Peut-on dire qu’il s’agit d’une base vers d’autres mathématiques ? Elles ne figurent pas dans le texte, et ne sont pas même entre aperçues. Avec la même prolixité que le traitement chez Clavius, les encyclopédies baroques du XVII^e siècle, pour l’essentiel des jésuites, développeront tout au contraire les exemples d’application aux sciences mixtes³⁵. Au final, les Éléments d’Euclide de Clavius peuvent se décrire comme un manuel auto-suffisant. Le contenu – en gros celui des Éléments – semble faire un corps qui ne renvoie à rien d’autre, mais il est suffisant aussi pour qui ne veut pas faire profession de mathématicien. L’adjectif élémentaire serait mal choisi pour un tel « tout », qui crée une contrainte intellectuelle considérable. Ainsi Clavius n’adopte-t-il pas l’usage de la perspective visuelle si satisfaisante qui faisait la splendeur de l’édition de Federigo Commandino, il ne choisit pas non plus l’abstraction foisonnante de Ratdolt, mais il adopte l’image faite par Grynaeus : on le voit par la réunion des illustrations 10, 11 et 12. C’est que la perspective comme théorie mathématique ne fait pas partie du « tout » que Clavius veut établir. Il ne veut donc pas que son traité par les images fasse appel à une théorie qui n’y est pas développée, aussi élémentaire soit-elle. Même si la technique de dessin de Commandino n’est peut-être pas si facile à justifier, aussi jolie paraisse-t-elle, nulle part n’est précisé où est le point de vue qui fait la projection : une perspective cavalière est sans doute en cause. Je ne crois pas avoir lu en tout cas d’études à ce sujet. Si Clavius a de bonnes raisons de se méfier, il sait que bien qu’inutile à la compréhension abstraite d’Euclide, la figure fait partie des aides de la mémoire. Aussi choisit-il, pour cette proposition de construction d’un polyèdre dans une sphère, dont la démonstration est la plus longue de toutes les propositions des Éléments, un dessin suggestif, mais visuellement non satisfaisant parce qu’aussi bien c’était le choix de l’imprimeur de la première version imprimée en grec.

Du point de vue de la « série » livresque envisagée, une autre singularité apparaît avec l’édition des « six premiers livres géométriques d’Euclide avec les démonstrations » due à Jacques Peletier du Mans en 1557³⁶. Le ton de ce mathématicien poète, qui avait choisi une vie de vagabond abandonnant la voie professorale universitaire garantie par sa famille, tout en étant délibérément un mathématicien professionnel, est en effet aussi bien celui d’un philosophe qui médite et réforme.

En somme, les Problemes sont comme certaine matiere & practique de l’art, de laquelle les Theoremes sont la forme & la méditation de la science³⁷

Voici son commentaire « figuré » à partir du rayon mobile, une fois la définition d’un cercle pourvue à la manière euclidienne à partir d’un diamètre, et que le traducteur appelle la « faction » ou création du cercle (voir aussi sa construction d’un cercle) :

Cercle, est la trace ou vestige d’une ligne droite, ayant une des extrémités fixe, & menée tout autour sus un plan, iusqu’à ce qu’elle retourne la mesme d’où elle a commencé a estremenée³⁸.

Peut-on associer à l’édition de Jacques Peletier, qui est en latin, la première version en anglais de ces Éléments, due à Henry Billinsgley ? Celle-ci s’ouvre par une longue préface de John Dee, cet astrologue si versatile de la reine Élisabeth. La version anglaise présente une innovation de choix pour un historien du livre, car elle fournit des modèles qui peuvent être dépliés pour faire comprendre les polyèdres ou plus généralement la géométrie dans l’espace dont on vient de voir chez Clavius les difficultés visuelles qu’elle comporte. Ces corps établissent chez Billinsgley le lien épistémologique entre la théorie euclidienne « fidèlement reproduite » selon le titre de l’ouvrage, et une pratique des arts entendus au-delà de l’art pictural. John Dee, qui reprend l’idée sempiternelle d’un ornement de l’esprit de l’homme, parle aussi de knowledge of good artes and sciences. Il n’oublie pas, peut-être avec une pointe d’ironie, de saluer au passage Lady Philosophie et Queene Theologie. Mais Billinsgley n’en dit pas un mot, pas plus qu’Euclide. Dee en profite pourtant pour donner une charte classifiée des sciences mathématiques, mettant Euclide en ouverture, plutôt qu’en manuel pour étudiants soucieux d’en finir avec l’imposition du quadrivium. Ne retrouve-t-on pas ici la suite de Finé, et la vraie différence avec Clavius ? Dee n’a pourtant pas publié un texte que l’on dit réformateur et qu’il avait enseigné au collège de Reims à Paris, portant comme Peletier de fait sur les seuls deux premiers livres d’Euclide : Prolegomana et dictata Parisiensia in Euclides Elementorum Geometricorum Librum et Secundum in Collegio Rhemensi. Cette restriction même à deux livres, sans ouverture pour autre chose, doit être mise en corrélation avec le peu d’attention pour ces mathématiques dans les universités d’alors, et dont l’apprentissage serait ainsi restreint à une sorte de teinture logique.

Les spécialistes d’Euclide, soucieux de la fidélité au texte grec, préfèrent signaler la publication en 1572 des Éléments d’Euclide par Federigo Commandino³⁹. Il me semble qu’il faudrait ajouter, du point de vue de l’histoire des sciences, que cette magnifique production, dont les images dans l’espace sont tellement soignées, fait partie d’une série des travaux commentés sur les œuvres antiques, d’Archimède, de Pappus, mais aussi bien d’Aristote sous la forme des Mechanica, dont il sera question un peu plus loin. Ces œuvres sont publiées en vue d’une réinterprétation du fonds antique, et elles participent de l’élan scientifique et technique d’un renouveau qu’une cour princière comme celle d’Urbino pouvait protéger, sans nécessaire visée universitaire. À cette cour œuvrait un « ingénieur » docte comme Guidobaldo del Monte, que nous allons bientôt retrouver pour les Mechanica. Cet effet de cour est peut-être parallèle à l’action du grand-duc de Florence qui invitait Galilée en 1610, après la publication du Messager des étoiles, quoiqu’il puisse sembler que la partie de philosophie naturelle y soit plus présente. L’attitude à Urbino est en tout cas voisine de ce qui se passait à la cour de Turin, où un Benedetti publiait en 1553 une série de problèmes issus notamment d’Euclide⁴⁰ avant, dans un second ouvrage, d’aller de la perspective à la chute des corps⁴¹. Il ne se souciait pas d’une fidélité au texte d’Euclide, ni même d’un enseignement. L’histoire culturelle peut ainsi signaler l’invention du livre de recherche, qualificatif qui vaudrait aussi bien pour l’Arithmétique de Stevin de 1585 – avant donc que ce dernier entre dans l’entourage de cour de Maurice de Nassau.

Il est une autre façon de rester dans la lignée de l’histoire du livre avec les Éléments, tout en offrant une perspective cognitive et culturelle. En effet, dans la série justement étiquetée Éléments, et qu’ils soient en latin ou non, se présente un jeu étrange sur les titres. On a en effet hésitation entre des titres comme Éléments d’Euclide, Éléments géométriques d’Euclide, voire plus rarement Éléments mathématiques d’Euclide, comme à Paris en 1545, Euclidis elementa mathematica. Clavius maintient la version que je peux dire philologique : Euclidis Elementorum libri XV, alors que Zamberti intitule EuclidesElementorumGeometricorum lib. XV, cum expositioneTheonis, à la façon de Finé en 1536 dans son In sex priores libros geometricarum elementorum Euclides. À l’intérieur même du texte, Clavius parle pourtant de Commentaria in Euclidis Elementa Geometria, et sa célèbre introduction s’intitule In disciplinismathematicasprologomenas, alors que sa préface se présente comme Euclidis elementa Praefatio. Commandino maintient Euclidis Elementorum libri XV, là où Dasypodius résiste par un Euclidis quindecim elementorum geometriae. Et un auteur comme Foix de Candalle publiant en 1566 à Paris mélange un peu le tout : EuclidisMegarensismathematiciclarissimielementageometrica, libris XV. Au titre s’ajoute, dans le joli style des humanistes, ad Germanam geometriae intelligentiam è diuersis lapsibus temporis iniuria contractis restitua…, mais le mot mathématiques n’apparaît que pour la profession d’Euclide, alors que c’est le mot géométrie qui vient ensuite. Par ces titres, les filiations déjà indiquées se dessinent, mais se manifestent des intentions différentes, pour des lectorats distincts.

L’hypothèse que l’on peut d’emblée faire est que l’appellation géométrique correspondrait à la restriction aux six premiers livres, et donc à une destination universitaire pour laquelle le quadriuium requérait justement la géométrie, comme Finé le faisait dans In sexprioreslibrosgeometricorumelementorumEuclides. Mais il y a trop d’exceptions pour que cela tienne sur le long terme. Une remarque de John Dee ne doit pas être prise à la légère, selon laquelle il ne faudrait plus appeler géométrie cette science qui s’occupe en fait des grandeurs, mais lui donner le nom de megethologia, à partir du grec (megete) pour grandeur. Effectivement la définition usuelle des mathématiques au XVII^e siècle allait devenir la science des grandeurs, puis la science des quantités susceptibles de plus ou de moins, et par conséquent le qualificatif de géométrie aurait dû être de moins en moins utilisé. Ce serait compter sans le développement du calcul algébrique, puis du calcul différentiel et intégral, qui en éliminant certes la théorie des proportions du livre V des Éléments d’Euclide traitée dans ses Éléments dits géométriques, se basait néanmoins sur la formalisation de celle-ci, celle dont on a vu un tout petit début avec le tableau de Clavius (ill. 13). On sait par ailleurs que les livres devant présenter le calcul différentiel et intégral au XVIII^e siècle durent poser en premier des rappels sur les coniques, du moins en les présentant selon les méthodes de la geometria organica, c’est-à-dire avec les équations algébriques et l’habitude des coordonnées introduites depuis Descartes en 1637, mais en faisant cependant jouer des propriétés présentées géométriquement, et non algébriquement, comme la conjugaison des diamètres. Ce qui prouve assez bien que les coniques ne faisaient pas partie du programme normal de l’enseignement, pas plus à l’université que dans les collèges, et a fortiori étaient largement absentes au XVI^e siècle, et ce malgré l’édition absolument remarquable jouant de la perspective de Commandino.

Un autre cas assez bien documenté : les éditions et les commentaires sur les Questiones mechanicæ attribuées à Aristote au XVI^e siècle. Il fallut attendre les années 1960 pour que deux érudits, l’un venant du monde lettré classique et l’autre du monde de l’histoire des sciences, s’associent pour une étude dite préliminaire, malheureusement jamais transformée en livre, prenant pour objet un texte, les Mekanika, que la tradition attribue à Aristote⁴², et que je préfère traduire comme « Problèmes sur les Mécaniques », respectant le sens latin des Questiones mechanicae. Le texte⁴³ comporte trente-cinq questions qui vont des rames, de la balance, et du levier, à la question de savoir pourquoi les choses lancées arrêtent de se mouvoir, mêlant des questions théoriques sur l’infini, comme ce que l’on a appelé la roue d’Aristote, avec la question de savoir pourquoi les galets de mer sont arrondis, ou encore pourquoi les corps ronds sont plus faciles à mouvoir. Par l’ancienneté du texte, puisqu’il est évidemment pré-euclidien, et par sa difficulté même, l’érudition s’évita de penser que la forme n’en était pas axiomatique, et peu archimédienne. Était-elle d’ailleurs pensée au XVI^e siècle comme forme mathématique ?

La question n’est ni maladroite, ni anachronique, mais en ce seul sens que le mot « mathématiques » en ce siècle, et d’ailleurs plus encore au suivant, désignait non pas un exposé à la mode euclidienne, mais un compendium de diverses sciences dites mixtes. En tout cas, lorsque Vossius au XVII^e siècle s’exerça à une compilation des ouvrages utiles à la connaissance scientifique, il fit un regroupement de ces ouvrages sur les mécaniques, pratiquement celles que retrouvent Rosen et Drake au XX^e siècle. Ces auteurs ne mentionnent d’ailleurs pas Vossius, passé aux oubliettes de l’histoire. Du coup, les auteurs qui parlent de « géométrie » peuvent vouloir signifier un grand respect des procédures archimédiennes, surtout basées sur la méthode d’exhaustion du livre V, et du raisonnement par l’absurde, à la différence de ceux qui suivent les Mécaniques d’Aristote et la classification des machines simples. Mais il ne faudrait pas prendre la voie néo-aristotélicienne dans les Mécaniques pour un nouveau dogmatisme. Elle est bien plus un questionnement, et l’expression de doutes, comme le montre la paraphrase qui devient la règle – on peut le vérifier dans la liste donnée en annexe. Cette fois, si l’on peut dire, il n’y aura pas de Clavius pour fixer un « tout » avec les mécaniques.

La question ici débattue ne pouvait être celle de caractériser les formes du livre mathématique, puisqu’il était en évolution forte. Il a donc d’abord fallu manifester comment son indéniable spécificité dans l’abstraction et l’intelligibilité empêcha la plupart des historiens de la culture de saisir le rôle de ce type de livres dans le voir et le sentir d’une période comme le XVI^e siècle. Pour le retrouver, bénéficiant de l’étude de séries, il était donc utile de souligner le rôle de certaines formes, comme la perspective mais aussi les tableaux numériques et les formules algébriques, et ainsi de comprendre une indéniable mathématisation des mentalités, alors même que la culture mathématique restait faible – comme le montre la large ignorance des coniques. Cette acculturation quasiment ordinaire ne pouvait que faciliter la révolution qui viendra dans le dernier tiers du XVII^e siècle.

Entre temps, mais en retour, la spécificité démonstrative globalement ordonnée des mathématiques ne pouvait que conduire à se méfier de l’emploi de ces trois techniques intellectuelles, au fond assez voisines épistémologiquement par l’usage de la spatialisation. Cette forme de handicap n’en fut peut-être pas un, obligeant les esprits à mieux fixer le rôle de l’analytique. La réunion de l’analytique et du spatial ne porte-t-il pas un nom, celui de géométrie analytique. Il ne fut trouvé que bien plus tard, à la fin du XVIII^e siècle, lorsque précisément furent oubliées les péripéties baroques qui ont été évoquées.

ANNEXE 1 – LES MECHANICA JUSQU’EN 1625

Éditions du texte grec

1497 : Opera Aristotelis, II, section IV, Venise, Alde Manuce (rééditions diverses). Mise au point du texte grec sur les manuscrits du Cardinal Bessarion, mais sans diagrammes.

1531 : in Aristotelis Opera Omnia, Bâle, édition de Erasme-Grynaeus.

1566 : Pierre de la Ramée ( ?), texte grec publié par A. Wechel à Paris, reproduit dans Aristotelis Opera chez les héritiers de Wechel à Francfort/Main en 1587. A peut-être été utilisé par Ramus pour ses cours annoncés en 1564 sur les Mechanica en tant que professeur royal.

Traductions

Édition, traduction latine et commentaire : 1599, Henri de Monantheuil (1536-1606), Aristotelis Mechanica graeca, emendata, latina facta, et commentariis illustrata, Paris, chez Jérémie Perier. Une édition aussi à Leyde la même année, et une autre édition à Lyon en 1600.

Traduction, 1517 : latin dû à Vittore Fausto (1480-1551). Aristotelis Mechanica (...) in pristinum habitum restituta ac latinitate donata, Paris. Sept diagrammes sont inclus. Une préface. Traduit vraisemblablement à partir de l’editio princeps (elle n’est pas mentionnée). Dédicace à l’ambassadeur de la République de Venise en France, Giovanni Baldoer. Texte plusieurs fois réédité, donc assez largement disponible.

Traduction et commentaires, 1525 : latin dû à Niccolò Leonico Tomeao (1456-1531), Conversio Mechanicarum Questionum Artistotelis cum Figuris, et Annotationibus quibusdam. Figure dans un recueil d’opuscules du même auteur (avec d’autres sur les questions naturelles et sur le Timée selon Proclus), publié à Venise par Bernardinus Vitalis. Une préface datée de Padoue, des diagrammes et des commentaires (dite plus tard adnotatiunculae). Nouvelle édition à Paris en 1530, chez Simon Colin, avec les Naturalia. Nombreuses rééditions au XVI^e siècle, et même XVII^e siècle, mais sans les diagrammes et sans les commentaires. C’est la version de diffusion.

Manuscrit non édité à l’époque : 1545, Diego Hurtado de Mendoza, Mechanica de Aristotiles. L’auteur (1503-1575) fut ambassadeur de l’Empire des Habsbourg à Venise de 1539 à 1546, visiteur à Padoue, et collectionneur informé de manuscrits grecs. Il traduit en assistant au Concile de Trente. Longue préface, critique du manque de connaissance mathématique de la traduction de 1525. Est motivé par la difficulté de joindre l’utilité pratique et les mathématiques.

Commentaires

Commentaire partiel : 1546, Niccolò Tartaglia (1500-1557), dans Questioed Inventioni Diverse, Venise, chez N. Bascarini. Il fait intervenir un dialogue avec Mendoza. Réédition en 1554. Traduction allemande non complète en 1558 par Walter Ryff, Der Fürnembsten, notwendigsten der gantzen Architectur angehörigen mathematischen und mechanischen Kunst,à Nuremberg, rééditée en 1629 parmi d’autres textes.

Commentaire, 1547 : Alessandro Piccolomini (1508-1579), In Mechanicas Quaestiones Atristotelis Paraphrasis paulo quidem plenior, Rome, chez A. Bladus. L’auteur fréquente Padoue autour de 1540, et paraphrase à la demande de Mendoza. Nouvelle édition sous le même titre à Venise en 1565, par Traianius Curtius. Traduction en italien en 1582 par Oreste Vannocio Biringucci : Parafrasi di Monsignor Alessandro Piccolomini (...) sopra le Mechaniche d’Aristotile, à Rome chez Francesco Zanetti. Mais n’a pas été traduit en italien l’appendice au commentaire fourni par Piccolomini, et intitulé De certitudine mathematicarum : il porte sur la validité des « sciences mixtes », selon l’orthodoxie aristotélicienne.

Cet opuscule de 1547 suscite une polémique avec Francesco Barozzi, qui publie à Padoue en 1560 Oratio de certitudine mathematicarum. C’est ce contexte qui crée le lien entre la démonstration mathématique et ses qualités et les Mechanica, donc la physique. Utilisation de diagrammes, et référence explicite au livre X de Vitruve en ce qui concerne la poulie. La version italienne contient un traitement de la vis, qui n’est pas chez le pseudo-Aristote, pris du Liber Mechanicorum (1577) de Guidobaldo del Monte, texte également mis en italien en 1581.

Traduction partielle et commentaire, en manuscrit 1569, en édition 1613 : Francisco Maurolico (1494-1575), Problemata mechanica cum appendice, et ad magnetem, et ad pixidemnauticampertinentia, à Messine. Maurolyco annonçait en 1540 son intention de publier et d’éditer de nombreuses œuvres, dont les Mechanica (lettre au cardinal Bembo).

Commentaire partiel sur les questions liées à la navigation (rames et gouvernail), 1566 : Pedro Nuñes, in De Arte atque ratione navigandi libri duo, Opera, à Bâle en 1566 ; à Coïmbra en 1573, les deux fois sous le titre In Problema mechanicorum Aristotelis de motu navigii ex remis annotatio una. Traduction en italien et commentaire, 1573 ; l’ingénieur du duc d’Este, Antonio Guarino (1504-1590), Le mechanice d’Aristotile, trasportate di Greco in volgareidioma, Modène, chez Andrea Gadalino.

Commentaire partiel et critique sur des questions particulières des Mechanica, 1585 : Giovanna Battista Benedetti (1530-1590), Diversarum speculationum mathematicarum et physicarum liber, Turin (réédition à Venise en 1586 et 1599).

Commentaire et développement, 1582, Bernardino Baldi (1553-1617) : In Mechanica Aristotelis Problemata Exercitationes, Mayence, chez J. Albinus. Liens déclarés des Mechanica avec Vitruve. Préface explicative et diagrammes. Édition à Mayence encore en 1621.

Commentaire partiel, 1615 : Giuseppe Biancani, Aristotelis loca mathematica ex universis ipsiusoperibus collecta et explicata, Bologne, chez B. Cochium.

Commentaire partiel, 1627 : Giovanni de Guevarra, Aristotelis mechanicas commentarii, Rome.

Mention des Mechanica

Édition par Philander du De Architectura de Vitruve en 1544.

Édition par Daniele Barbaro en italien du De Architectura de Vitruve à Venise en 1566.

Mention indirecte dans John Dee, Euclid, 1570.

Cours attestés sur les Mechanica à Padoue par Catena à partir de 1548, par Giuseppe Moleto en 1581 (manuscrit disponible à l’Ambrosiana à Milan) se référant à la traduction de Fausto.

Speroni, pour un curriculum d’architectes, mentionne les Mechanica à Padoue.

Mention des Mechanica dans Archimedis (...) paraphrasis de Guidobaldo del Monte, 1588.

Selon la tradition, Galilée dut enseigner sur les Mechanica à Padoue en 1598 (plusieurs manuscrits). Une sorte de principe de conservation est envisagé par Galilée vers 1600, allant contre le « miracle » aristotélicien de la mécanique (ce qui est gagné en puissance est perdu en temps ou en espace). Mention par Galilée des Mechanica en 1612, à propos des vitesses virtuelles, sur son travail sur les corps flottants.

Mention en particulier des Mechanica dans les éditions de livres sur les machines comme Vittorio Zonca (Nova teatro di machine e edifici, 1607), ou Buonaioto Lorini sur les fortifications en 1609.

ANNEXE 2 – ÉDITIONS DES ÉLÉMENTS D’EUCLIDE EN FRANÇAIS ET EN ANGLAIS AVANT 1615

En français

Les Six premiers des Eléments d’Euclide traduicts et commentez par P. Forcadel de Béziés, Paris, H. de Marnef et G. Cavellat, 1564, in-4°, [2-]190 f.

Les Neuf livres des Elémens d’Euclide, trad. P. Forcadel, Paris, de Marnef, 1564, in-4°, 190 f., fig.

Le Septième, huictième et neusième livres des élémens d’Euclide, comprenans toute la science des nombres, traduicts et commentez par Pierre Forcadel de Beziés, Paris, C. Périer, 1565, in-4°, 122 p.

Les Six premiers Livres des Eléments d’Euclide traduicts par P. Forcadel de Béziés, Paris, C. Perier, 1566, in-8°, 31 p.

Les Six premiers des Eléments d’Euclide traduicts et commentez par P. Forcadel de Bézié, Paris, H. de Marnef et G. Cavellat, 1569, in-4°, 190 f.

Les Six premiers des Elemens d’Euclide : traduicts et commentez par J. Errard, Paris, 1598, in-8°, 48 f.

Les Six premiers des Elemens d’Euclide : traduicts et commentez par J. Errard de Bar-le-Duc, Paris, G. Auvray, 1604, in-8°, 90 f.

Les Eléments de la géométrie d’Euclide Mégarien. Traduicts et restitués à leur ancienne brèveté, selon l’ordre de Theon. Auxquels ont este adjoutez les quartorze et quinziesme d’Ipsicles, (...). Le tout par Dounot de Bar-le-Duc, Paris, J. Le Roy, 1609, in-4°, 264 p. Il y a une autre édition en 1610 (même pagination) et en 1613 (272 pages).

Les Six premiers livres des Eléments géométriques d’Euclide avec les démonstrations de Jacques Peletier du Mans, traduicts en français, Genève, Jean de Tournes, 1611, in-4°, [2-]299 p.

Les Quinze livres des Éléments d’Euclide, traduicts de latin en français (...), par Didier Henrion, A. Pacard, J. A. Joallin, Paris, Abraham Pacard, Jean Anthoine Joallin, 1614, in-8°, [1, 1b l., 16-]621[-14 l.] p.

En anglais

Robert RECORDE, The Pathway to Knowledge, containing the first principles of geometrie, as they moste aptly be applied unto practice (...), [imprinted in London, in Pavles churcheyarde (...) by Reynold Wolfe], 1551, 4°, 1551, [92] f.

The Elements of geometry of the most ancient philosopher Euclide of Megara. Faithfully (now first) translated into the Englishetoung, by Henry Billingsley, Citizen of London. With a fruitfull Praeface made by M.I. Dee, specifying the chiefemathematical Sciences, Londres, John Daye, 1570, in-2°, [28-]464 p.

Robert RECORDE, The Pathway to Knowledge, R. Woolfe, 1574, in-4°, 92 f., diagrammes dans le texte. Une troisième édition a lieu en 1602.

CAHIER ICONOGRAPHIQUE

Illustrations 1 et 2. Le « programme » de publication de « l’algèbre nouvelle » de François Viète en 1591 tel qu’il est dressé dans Francisci Vietae in artem analyticem isagoge, ouvrage publié à Tours chez Jamet Mettayer ; structuration spatiale d’un bout de page dans ce même ouvrage, avec notes manuscrites d’un lecteur assidu (exemplaire de la Bibliothèque nationale).

Illustrations 3 et 4. Une page complète du Canon mathematicus seu ad trianguli cum Appendicibus de François Viète, ouvrage publié à Paris par Jean Mettayer. Une page de la « table d’intérêt » de Simon Stevin publié en flamand en 1582 chez Christophe Plantin à Anvers (d’après The Principal Works, disponible sur le Net).

Illustrations 5 et 6. Frontispice par Francesco Curti dans l’ouvrage de Riccioli en 1651, « Le Nouvel Almageste » publié en latin à Bologne. Frontispice d’un ouvrage de Dou à Leyde en édition de 1620.

Illustration 7. Frontispice de « L’Essayeur » de Galilée en 1623, avec les deux personnifications opposées.

Illustrations 8 et 9. Le célèbre frontispice des « Tables Rudolphines », dessiné et gravé par Georg Celer en 1627, et la copieuse page de titre de l’ouvrage.

Illustrations 10, 11 et 12. Figures de la proposition 17 du livre XII des Éléments d’Euclide, respectivement chez Ratdolt en 1482, dans l’editio princeps de Grynaeus en 1533, et dans l’édition latine par Commandino à Pesaro en 1572.

Illustration 14. Un tableau inséré par Clavius au livre V de son Commentaire des Éléments d’Euclide (1591)

Illustration 16. Un extrait de l’Euclide de Pierre de la Ramée, publié à Paris en 1549.

Illustration n° 1 – Francisci Vietæ in artem analyticem isagoge, seorsim excussa ab Opere restitutæ Mathematicæ Analyseos, seu, Algebra noua, Turonis, apud Iametium Mettayer typographum regium, 1591, f. A1v. BnF, Réserve des livres rares, V-1507.

Illustration n° 2 – Francisci Vietæ in artem analyticem isagoge, seorsim excussa ab Opere restitutæ Mathematicæ Analyseos, seu, Algebra noua, Turonis, apud Iametium Mettayer typographum regium, 1591, f. B2v. BnF, Réserve des livres rares, V-1507.

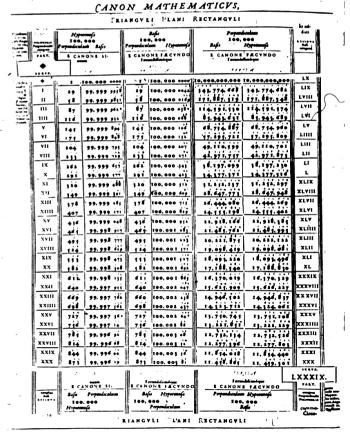
Illustration n° 3 – Canon mathematicus seu ad Triangula cum Adpendicibus, Lutetiae, apud Ioannem Mettayer, in Mathematicis Typographum Regium, sub signo D. Ioannis, e regione Collegii Laodicensis, 1579, f. c1v. © Bibliothèque de Bâle.

Illustration n° 4 – Tafelen van interest, mitsgaders de constructie der selver, gecalculeert door Simon Stevin, Bruggelinck, T’Antwerpen by Christoffel Planty, in den gulden Passer, 1582 (sur le Net).

Illustration n° 5 – Almagestum nouum astronomiam ueterem nouamque complectens obseruationibus aliorum, et propriis nouisque theorematibus, problematibus, ac tabulis promotam, in tres tomos distributam (...), auctore P. Ioanne Baptista Ricciolo, Bononiae, ex typ. Hrdi V. Benatii, 1651, frontispice gravé. 375A (Gallica).

Illustration n° 6 – Tractaet vant maken ende gebruycken eens nieu gheordonneerden Mathematischen Instruments, In welcke vercheyden konstighe stucken (...) door Ian Pieterszoon Dou (...), Amsterdam, by Willem Ianssen op’t Water, 1620 : page de titre (Bayerische Staatsbibliothek, Math. a. 70m).

Illustration n° 7 – Il saggiatore nel quale con bilancia esquisita e giusta si ponderano le cose contenute nella libra astronomica e filosofica di Lotario Sarsi Sigensano scritto in forma di lettera all’Illmo (...) Virginio Cesarini (...) dal Sigr. Galileo Galilei (...), In Roma appresso Giacomo Mascardi, 1623 : page de titre (BU Gand, Res. 710).

Illustration n° 8 – Tabulae Rudolphinae, quibus astronomicae scientiae, temporum longinquitate collapsae restauratio continetur, a Phoenice illo astronomorum Tychone, ex illustri & generosa Braheorum in regno Daniae familia oriundo equite, primum animo concepta et destinata anno Christi MDLXIV (...), Ulm, Jonas Saur, 1627 : frontispice. ETH-Bibliothek Zürich, Rar 8895 q (e-rara http://dx.doi.org/10.3931/e-rara-8742)

Illustration n° 9 – Tabulae Rudolphinae, quibus astronomicae scientiae, temporum longinquitate collapsae restauratio continetur, a Phoenice illo astronomorum Tychone, ex illustri & generosa Braheorum in regno Daniae familia oriundo equite, primum animo concepta et destinata anno Christi MDLXIV (...), Ulm, Jonas Saur, 1627 : page de titre. ETH-Bibliothek Zürich, Rar 8895 q (e-rara http://dx.doi.org/10.3931/e-rara-8742)

Illustration n° 10 – Elementa geometriae, Venise, Erhard Ratdolt, 25 May 1482, f° 8. Bibliothèque Sainte-Geneviève, Paris, OEXV 231 RES (Archive.org).

Illustration n° 11 – Εωκλείδου Στοιχείων βιβλ. ιε’ έκ των Θέωνος συνουσιων (...), Basileae, apud J. Hervagium, 1533, 198 feuilles.

Illustration n° 12 – Euclidis elementorum libri XV. Vnà cum scholijs antiquis. A Federico Commandino Vrbinate nuper in Latinum conuersi, commentarijsque quibusdam illustrati, Pisauri, Iacobus Chriegher German., 1572, f. 225. BM Lyon 104408 (© Google Books).

Illustration n° 13 – Euclidis elementorum libri XV. Accessit XVI de solidorum regularium cuiuslibet intra quodlibet comparatione (...), auctore Christophoro Clavio Bambergensi, e societate Iesu, Coloniae, expensis Ioh. Baptistae Ciotti, 1591.

____________

¹ Le seul livre à ce propos, heureusement conséquent, m’a paru être celui paru sous la direction de Cynthia Hay, Mathematics from Manuscripts to Print, 1300-1600, Oxford, Clarendon Press, 1988. Il y a d’autres productions, depuis longtemps sous la forme d’articles et urtout de listes de livres mathématiques, dont la plus notable me paraît être celle de Diana M. Simpkins, « Earlyeditions of Euclid in England », dans Annals of Science, 22, n° 4 (dec. 1966), p. 225-249, car elle mentionne la taille des ouvrages, les imprimeurs et les libraires, etc.

² Histoire de l’édition française [ci-après HEF], I : Le Livre conquérant : du Moyen Âge au milieu du XVII^e siècle, dir. Henri-Jean Martin, Roger Chartier, en collab. avec Jean-Pierre Vivet, Paris, Promodis, 1983.

³ A fortiori furent donc négligées les études qui pouvaient porter sur la modification de forme des textes mathématiques sous la longue influence arabe.

⁴ Art and the printed book, 1455-1955 de Joseph Blumenthal, quatrième édition en 1984, ne cite que le livre de perspective de Jean Cousin de 1560 (repris d’ailleurs dans l’Histoire de l’édition française) et le frontispice de l’Arithmetica practica d’Oronce Finé.

⁵ Francisci Vietæ in artem analyticem isagoge, seorsim excussa ab Opere restitutæ Mathematicæ Analyseos, seu, Algebra noua, Turonis, apud Iametium Mettayer typographum regium, 1591, in-2°. Il faut seulement déchiffrer Apl comme désignant une grandeur d’homogénéité deux comme une aire, et la règle donne à calculer selon 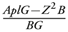, comme on peut le voir et comme le scripteur l’indique en marge.

⁶ Michel Pastoureau, « L’illustration du livre : comprendre ou rêver ? », dans HEF, I, p. 501-529.

⁷ Un ouvrage particulièrement utile lorsqu’il n’y avait pas encore les moyens actuels de repérer les ouvrages est le travail de Robin Rider, A Bibliography of Early Modern Algebra, 1500-1800, Berkeley, University of California, 1982, et l’accompagnement par des expositions à ce propos. Des travaux plus anciens avaient systématiquement traqué les éditions et les traductions en langue vernaculaire des Éléments d’Euclide.

⁸ Voir Jackie Stedall, A Discourse Concerning Algebra. English Algebra to 1685, Oxford, Oxford University Press, 2002.

⁹ En témoigne un article de Domenico Bertoloni Meli sur leur rôle pour le travail d’expérimentation (2004), paru dans Perspectives on Science, 12, 2 (2004), p. 164-190, un an après un livre paru à Oxford, sous la direction de Martin Campbell-Kelly, The History of Mathematical Tables: From Science to Spreadsheets.

¹⁰ Tafelen van interest, mitsgaders de constructie der selver, gecalculeert door Simon Stevin, Bruggelinck, T’Antwerpen, by Christoffel Planty, in den gulden Passer, 1582.

¹¹ On n’a pas toujours signalé que les tables numériques de logarithmes, que l’on voit paraître sous la plume de Napier en 1614 et qui circulent partout en Europe, et en Chine aussi bien, sont bien antérieures aux dessins de la courbe logarithmique (ou exponentielle).

¹² Certaine errors in nauigation, arisingeither of the ordinari eerroneous making or vsing of the seachart, compasse, crosse staffe, and tables of declination of the sunne, and fixed starres detected and corrected , Printedat London, By Valentine Sims [and W. White], 1599.

¹³ Je n’ai pas voulu entrer dans le descriptif technique que l’on trouvera développé dans un livre qui doit paraître en 2013, Jean Dhombres, Les Savoirs mathématiques et leurs pratiques culturelles, Paris, Hermann, chapitre 7. Le lien entre mathématiques et voyages de découvertes comme cartographie est joliment développé dans Amir R. Alexander, Geometrical Landscapes, Stanford, Stanford University Press, 2002.

¹⁴ Henri-Jean Martin, Mise en page et mise en texte du livre français : la naissance du livre moderne, XIV^e-XVII^e siècles, collab. Jean-Marc Chatelain, Isabelle Diu, Aude Le Dividich, Laurent Pinon, Paris, Cercle de la librairie, 2000.

¹⁵ Voir Jean Dhombres, Patricia Radelet-de Grave, Une Mécanique donnée à voir : les thèses de statique défendues à Louvain en 1624 par Grégoire de Saint-Vincent, Turnhout, Brepols, 2009.

¹⁶ Almagestum nouum astronomiam ueterem nouamque complectens obseruationibus aliorum, et propriisnouisque theorematibus, problematibus, actabulis promotam, in tres tomos distributam (…), auctore P. Ioanne Baptista Ricciolo, Bononiae, ex typ. Hrdi V. Benatii, 1651.

¹⁷ Tractaet vant makenende gebruycken eens nieugheordonneerden Mathematischen Instruments, In welcke vercheyden konstighestucken (…) door Ian PieterszoonDou…, Amsterdam, by Willem Ianssenop’t Water, 1620.

¹⁸ Psaume 8, verset 4.

¹⁹ J’omets ici de gloser sur la cote d’armes, donc sur le patronage et le mécénat dont les universitaires se passaient le plus souvent, alors que les jésuites cherchèrent à partir du début du XVII^e siècle à systématiquement l’obtenir.

²⁰ Il Saggiator enel quale con bilancia esquisita e giusta si ponderano le cose contenute nella libra astronomica e filosofica di Lotario Sarsi Sigensanoscritto in forma di lettera all’Illmo (…) Virginio Cesarini (…) dal Sigr. Galileo Galilei…, In Roma appresso Giacomo Mascardi, 1623.

²¹ Traduction Jean Dhombres.

²² Volker Remmert, Widmung, Welterklärungund Wissenschafts legitimierung. Titel bilder und ihre Funktione in der wissenschaftlichen Revolution, Wiesbaden, HarrassowitzVerlag, 2005.

²³ Marc Fumaroli, « Ego scriptor : rhétorique et philosophie dans le Discours de la méthode », dans Problématique et réception du Discours de la méthode et des Essais, dir. Henri Méchoulan, Paris, Vrin, 1988, p. 31-46.

²⁴ Jean Dhombres, « Les enjeux de l’illustration du livre mathématique : Rubens et son école », dans Art et imagination scientifique à la Renaissance, Paris, Europia Productions, 2004, p. 51-78.

²⁵ Elementageometriae, Venezia, Erhard Ratdolt, 25 Mai 1482. ISTC ie00113000.

²⁶ Je signale d’emblée que les manuscrits et éditions d’Euclide ont fait l’objet d’une remarquable description synthétique de John Murdoch dans la première version du Dictionary of Scientific Biography (vol. 3), revue dans la deuxième édition. Par ailleurs les éditions des Éléments d’Euclide ont fait l’objet d’un travail de recensement, quoique incomplet, par Pietro Riccardi, « Saggio di una bibliografia Euclidea », dans Memorie della R. Accademia delle scienze dell’Istituto di Bologna, ser. 4, 8 (1887), 4e série, 9 (1887), 5e série, 1 (1889), 5e série, 3 (1893). Voir aussi G. Stanford-Thomas, Early editions of Euclid’s Elements, London, Bibliographical Society, 1926 (« IllustratedMonographsissued by the BibliographicalSocieyt », 20).

²⁷ Euclidis Megarensis philosophi Platonici mathematicarum disciplinarum ianitoris, habent in hoc volumine quicumque ad mathematicam substantiam aspirant, elementorum libros XIII cum exposition Theonis insignis mathematici, quibus multa quae deerant ex lectione Graeca sumpta addita sub nec non plurima subuersa & prepostere, voluta in Campani interpretatione…, [Impressum Venetiis, in aedibus Ioannis Tacuini librari iaccuratissima dilligentia recognitum, 1505].

²⁸ Euclidis Megarensis philosophi acutissimi mathematicorumque omnium sine controuersi principis Opera a Campano interprete fidissimo tralata (…) Lucas Paciolus theologus insignis, altissima mathematicarum disciplinarum scientia rarissimus iudicio castigatissimo detersit, emendauit…, [Venetiis], A. Paganius Paganinus characteribus elegantissimis accuratissime imprimebat, 1509.

²⁹ Geometricorum elementorum XV. In eosdem commentariorum libri XV. In tredecim priores, commentariorum libri XIII. In duos posteriores commentariorum libri II…, Parisiis, in officina H. Stephani, [1516].

³⁰ Εὐκλείδου Στοιχείων βιβλ. ιε ἔκ τῶν Θέωνοσσυνουσιῶν…, Basileae, apud J. Hervagium, 1533.

³¹ Orontii Finaei Delphinatis, regii mathematicarum Lutetiae professoris, In sex priores libros geometri- corum elementorum Euclidis : demonstrationes quibus ipsius Euclidis textus graecus suis locisinsertus est, una cum interpretatione latina Bartholomei Zamberti Veneti, ad fidem geometrica, per eundem Orontium recognita, Parisiis, apud Simonem Colinæum, 1536.

³² Voir Jean Dhombres, « La mise à jour des mathématiques par les professeurs royaux », dans Histoire du Collège de France, t. 1, La création 1530-1560, dir. A. Tuilier, Paris, Fayard, 2006, p. 377-420.

³³ Cette inutilité est-elle en quelque sorte prévue par les omissions de livres comme le livre X déjà chez Peletier ? Voir en annexe la liste des traductions des Éléments.

³⁴ Annexe 2 : liste des éditions des Éléments en français, p. 162-162. Voir Marie Lacoarret, « La traduction françaises des Œuvres d’Euclide », dans Revue d’histoire des sciences, 10 (1957), p. 38-58.

³⁵ Même dans ces encyclopédies, il y a de fortes différences, et il serait anormal de ranger pour le traitement d’Euclide dans le même genre ce que fera vers 1670 un Milliet de Chales à Lyon et ce que proposait Schott, fidèle disciple de Kircher qui est le véritable de l’idée d’une culture encyclopédique.

³⁶ Voir annexe 2.

³⁷ Je choisis la traduction française donnée en 1611 par Jean de Tournes, qui avait reçu enfant des leçons de Jacques Peletier du Mans. Je tire les citations des Six premiers livres des éléments géométriques d’Euclide avec les démonstrations de Jacques Peletier du Mans, Genève, Jean de Tournes, 1628.

³⁸ Ibid.

³⁹ Euclidis elementorum libri XV. Vna cum scholiis antiquis. A Federico Commandino Vrbinate nuper in Latinum conuersi, commentariisque quibusdam illustrati, Pisauri, Iacobus Chriegber German, 1572.

⁴⁰ Giovanni Baptista Benedetti, Resolutio omnium Euclidis problematum aliorumque ad hoc necessario inuentorum una tantu modo circini data apertura (…) per Joannem Baptistam de Benedictis inventa, Venetiis, apud B. Caesanum, 1553.

⁴¹ Diversarum speculationem mathematicarum et physicarum liber, Taurini, apud haeredem N. Bevi- laquae, 1585.

⁴² Paul Lawrence Rose, Stilmann Drake, « The Pseudo-aristotelian Question in Mechanics in Renaissance Culture », dans Studies in the Renaissance, 18 (1971), p. 65-103.

⁴³ Pseudo-Aristote, MEKANIKA, W. S. Hett, Aristotle, Minor Works,with an English translation, Mechanicalproblems, Cambridge, Mass., Harvard University Press, 1963 ; trad. ital. avec le texte grec, Maria Elisabetta Bottechia Dehò, Aristotele, Problemi meccanici, Soveria Mannelli (CZ), Rubbettino, 2000 ; il n’existe pas actuellement de version française, mais une bonne version espagnole datée de la fin du XIX^e siècle.